Transvection
A linear mapping 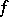 of a (right) vector space
of a (right) vector space 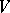 over a skew-field
over a skew-field 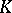 with the properties
with the properties
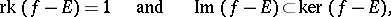 |
where 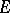 is the identity linear transformation. A transvection can be represented in the form
is the identity linear transformation. A transvection can be represented in the form
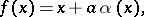 |
where 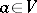 ,
, 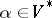 and
and 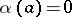 .
.
The transvections of a vector space 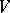 generate the special linear, or unimodular, group
generate the special linear, or unimodular, group 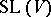 . It coincides with the commutator subgroup of
. It coincides with the commutator subgroup of 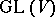 , with the exception of the cases when
, with the exception of the cases when 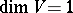 or
or 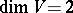 and
and 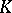 is the field of two elements. If
is the field of two elements. If 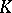 is a field, then
is a field, then 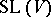 is the group of matrices with determinant 1. In the general case (provided that
is the group of matrices with determinant 1. In the general case (provided that  ),
), 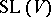 is the kernel of the epimorphism
is the kernel of the epimorphism
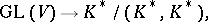 |
which is called the Dieudonné determinant (cf. Determinant).
References
| [1] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
Comments
In the projective space 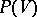 , whose points are the
, whose points are the 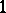 -dimensional subspaces of
-dimensional subspaces of 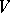 , a transvection
, a transvection 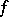 as above induces a (projective) transvection with
as above induces a (projective) transvection with 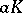 as centre and
as centre and 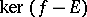 as axis. If one takes
as axis. If one takes 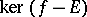 to be a hyperplane at infinity in
to be a hyperplane at infinity in 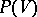 , such a transvection induces a translation
, such a transvection induces a translation 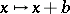 in the remaining affine space (interpreted as a linear space). See also Shear.
in the remaining affine space (interpreted as a linear space). See also Shear.
Transvection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transvection&oldid=16329