Transmission rate of a channel
An information-theoretic measure of the ability to transmit information over a communication channel. Let  and
and  be random variables connected in a communication channel
be random variables connected in a communication channel  . Then the transmission rate
. Then the transmission rate  of this channel is defined by the equation
of this channel is defined by the equation
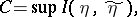 | (1) |
where  is the amount of information (cf. Information, amount of) in
is the amount of information (cf. Information, amount of) in  relative to
relative to  , and the supremum is taken over all pairs of random variables
, and the supremum is taken over all pairs of random variables  connected in the channel
connected in the channel 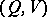 . In the case when the input and output signals
. In the case when the input and output signals 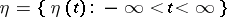 and
and  are random processes in continuous or discrete time, the transmission rate of the channel is usually understood to mean the mean transmission rate of the channel, taken in unit time or over one symbol of the transmitted signal, that is, by definition one sets
are random processes in continuous or discrete time, the transmission rate of the channel is usually understood to mean the mean transmission rate of the channel, taken in unit time or over one symbol of the transmitted signal, that is, by definition one sets
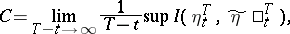 | (2) |
if the limit exists; here the supremum is taken over all possible pairs of random variables  ,
, 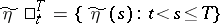 connected in the corresponding segment of the given channel. The existence of the limit (2) has been proved for a wide class of channels, for example for a homogeneous channel with a finite memory and non-vanishing transition probabilities.
connected in the corresponding segment of the given channel. The existence of the limit (2) has been proved for a wide class of channels, for example for a homogeneous channel with a finite memory and non-vanishing transition probabilities.
It is known that for a sufficiently wide class (for example, for the channels with finite memory mentioned above) the following holds:
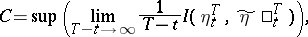 | (3) |
where the supremum is taken over all pairs of stationarily-related random processes 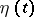 ,
, 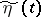 ,
,  , such that for any
, such that for any  the random variables
the random variables 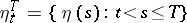 and
and  are connected in the corresponding segment of the channel under consideration. Thus, (3) shows that the transmission rate of the channel is the same as the maximum possible transmission rate of information (cf. Information, transmission rate of) along this channel.
are connected in the corresponding segment of the channel under consideration. Thus, (3) shows that the transmission rate of the channel is the same as the maximum possible transmission rate of information (cf. Information, transmission rate of) along this channel.
An explicit calculation of transmission rates is therefore of considerable interest. For example, for a channel 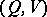 whose input and output signals take values in the Euclidean
whose input and output signals take values in the Euclidean  -dimensional space
-dimensional space 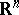 , with transition function
, with transition function  defined by a density
defined by a density 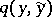 (with respect to the Lebesgue measure),
(with respect to the Lebesgue measure),  , and with the constraint
, and with the constraint 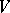 consisting of boundedness of the mean square power of the input signal,
consisting of boundedness of the mean square power of the input signal, 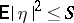 (where
(where 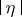 is the length of the vector
is the length of the vector 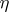 in
in 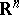 ),
), 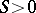 being a fixed constant, the following results are known (see ).
being a fixed constant, the following results are known (see ).
1) Let 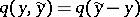 , that is, one considers a channel with additive noise such that the output signal
, that is, one considers a channel with additive noise such that the output signal 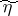 is equal to the sum
is equal to the sum 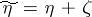 of the input signal
of the input signal 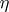 and a noise
and a noise  independent of it, and let
independent of it, and let 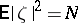 . Then as
. Then as 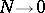 (under weak additional conditions) the following asymptotic formula holds:
(under weak additional conditions) the following asymptotic formula holds:
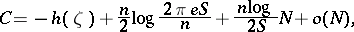 |
where  is the differential entropy of
is the differential entropy of 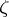 and
and  as
as 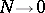 . This formula corresponds to the case of little noise.
. This formula corresponds to the case of little noise.
2) Let  be arbitrary but let
be arbitrary but let  . Then
. Then
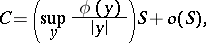 |
where
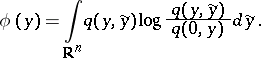 |
See also , – cited under Communication channel.
References
| [1a] | V.V. Prelov, "The asymptotic channel capacity for a continuous channel with small additive noise" Problems Inform. Transmission , 5 : 2 (1969) pp. 23–27 Probl. Peredachi Inform. , 5 : 2 (1969) pp. 31–36 |
| [1b] | V.V. Prelov, "Asymptotic behavior of the capacity of a continuous channel with large nonadditive noise" Problems Inform. Transmission , 8 : 4 (1972) pp. 285–289 Probl. Peredachi Inform. , 8 : 4 (1972) pp. 22–27 |
Comments
References
| [a1] | P. Billingsley, "Ergodic theory and information" , Wiley (1965) |
| [a2] | R.B. Ash, "Information theory" , Interscience (1965) |
| [a3] | A.M. Yaglom, I.M. Yaglom, "Probabilité et information" , Dunod (1959) (Translated from Russian) |
Transmission rate of a channel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transmission_rate_of_a_channel&oldid=17437