Translation of programs
The translation of programs in programming, also called compilation of programs, is a systematic process that transforms any program 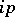 in the input algorithmic language
in the input algorithmic language 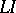 into some program
into some program 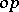 in the object language
in the object language 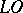 ; furthermore, both programs
; furthermore, both programs  and
and 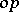 should realize the same function, that is, if
should realize the same function, that is, if 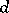 is the input data of the program, then
is the input data of the program, then 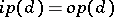 .
.
A translation of programs in the theory of computable functions and theory of algorithms (cf. Algorithms, theory of; Computable function) is any mapping of one enumeration of computable functions to another that preserves the property that the image and pre-image are the numbers of the same function (the presence of an effective translating mapping is also called reducibility of one enumeration to another).
In programming practice, the programming language used by the human being is usually the input language, while the object language is usually the language that is carried out directly by the machine programs. The translation of programs itself is, as a rule, carried out automatically, that is, by means of a program 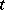 in some realization language
in some realization language 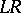 , called the translator (or compiler), that is,
, called the translator (or compiler), that is, 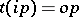 . The systematic development of translators for any input language
. The systematic development of translators for any input language 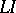 from some class of languages is what constitutes automatic programming, and the corresponding devices of such a development are called systems of compiler construction, or compilers of compilers,
from some class of languages is what constitutes automatic programming, and the corresponding devices of such a development are called systems of compiler construction, or compilers of compilers, 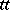 :
: 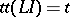 . Here, the realization language either contains the object language or coincides with it:
. Here, the realization language either contains the object language or coincides with it: 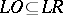 .
.
The notion of a translation of programs (reducibility) in the theory of computable functions leads to the notion of principal enumerations, that is, enumerations to which any other enumeration of some class can be reduced. The existence has been proved of principal computable enumerations for all concrete models of computable functions; in particular for partial recursive functions and for Turing machines. In turn, the existence of principal computable enumerations is enabled by the ability of computable functions to perform so-called partial computations, that is, by the existence of a general recursive function (in programming, a partial computer; in the theory of computable functions, an 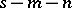 -function)
-function) 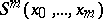 such that if
such that if 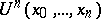 is a universal function for computable functions of
is a universal function for computable functions of  variables, then for any computable function
variables, then for any computable function 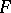 of
of 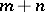 variables and with number
variables and with number 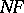 , one has the identity
, one has the identity
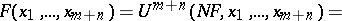 |
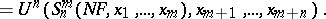 |
As is obvious from this identity, a partial computer constructs from a program of 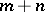 variables and given values of
variables and given values of  variables a program of a function of
variables a program of a function of  variables obtained from the original program by associating
variables obtained from the original program by associating 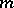 of its arguments with these values. The result of a partial computation is called the projection
of its arguments with these values. The result of a partial computation is called the projection 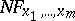 of the program
of the program 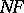 on the given values
on the given values 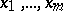 of
of 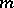 of its arguments. The existence of principal computable enumerations (see [1], Chapt. 1, Sect. 2) and partial computers (see [2], Sect. 65), as well as their connection (see [3], Sect. 11, Theorem 3) is one of the fundamental aspects of the theory of computable functions.
of its arguments. The existence of principal computable enumerations (see [1], Chapt. 1, Sect. 2) and partial computers (see [2], Sect. 65), as well as their connection (see [3], Sect. 11, Theorem 3) is one of the fundamental aspects of the theory of computable functions.
There is a direct relationship between problems of practical translation in programming and partial computations (see [4]). Suppose that the realization language 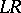 has a principal computable enumeration and let
has a principal computable enumeration and let 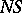 be the program of a partial computer for
be the program of a partial computer for 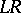 expressed in the same language. Suppose further that the input language
expressed in the same language. Suppose further that the input language 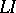 is defined by a program
is defined by a program 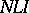 of its universal function expressed in an object subset
of its universal function expressed in an object subset 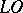 of
of 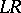 , that is,
, that is, 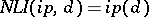 . (In programming, such a program is called an interpreter of the input language.) Then the following relations hold:
. (In programming, such a program is called an interpreter of the input language.) Then the following relations hold:
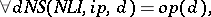 |
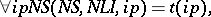 |
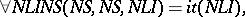 |
that is, the object program is the projection of the interpreter of the input language onto the input program; the compiler is the projection of the partial computer onto the interpreter of the input language; while the compiler of compilers is the projection of the partial computer onto itself.
References
| [1] | Yu.L. Ershov, "Theorie der Numierungen" , I-II , Deutsch. Verlag Wissenschaft. (1973–1976) (Translated from Russian) |
| [2] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
| [3] | V.A. Uspenskii, "Leçons sur les fonctions calculables" , Hermann (1966) (Translated from Russian) |
| [4] | A.P. Ershov, , All-Union Conference. Methods of mathematical logic in problems of artificial intelligence and systematic programming. Palanga, 3–5 Sept. 1980 , 2 , Vilnius (1980) pp. 26–55 (In Russian) |
Comments
References
| [a1] | N.D. Jones, "Partial evaluation, self-application and types" M.S. Paterson (ed.) , Automata, Languages and Programming (Proc. ICALP 17, Warwick, July 1990) , Lect. notes in comp. science , 443 , Springer (1990) pp. 639–659 |
Translation of programs. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Translation_of_programs&oldid=12660