Difference between revisions of "Transitive group"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 49016 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Permutation group|permutation group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938001.png" /> such that each element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938002.png" /> can be taken to any element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938003.png" /> by a suitable element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938004.png" />, that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938005.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938006.png" /> is the unique [[Orbit|orbit]] of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938007.png" />. If the number of orbits is greater than 1, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938008.png" /> is said to be intransitive. The orbits of an intransitive group are sometimes called its domains of transitivity. For an intransitive group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t0938009.png" /> with orbits <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380010.png" />, |
| − | t0938001.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380011.png" /></td> </tr></table> | |
| − | |||
| − | + | and the restriction of the group action to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380012.png" /> is transitive. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380013.png" /> be a subgroup of a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380014.png" /> and let | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380015.png" /></td> </tr></table> | |
| − | |||
| − | + | be the decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380016.png" /> into right cosets with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380017.png" />. Further, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380018.png" />. Then the action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380019.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380020.png" />. This action is transitive and, conversely, every transitive action is of the above type for a suitable subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380022.png" />. | |
| − | be a subgroup of | ||
| − | |||
| − | + | An action <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380023.png" /> is said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380025.png" />-transitive, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380026.png" />, if for any two ordered sets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380027.png" /> distinct elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380028.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380030.png" />, there exists an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380031.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380032.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380033.png" />. In other words, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380034.png" /> possesses just one anti-reflexive <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380035.png" />-orbit. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380036.png" />, a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380038.png" />-transitive group is called multiply transitive. An example of a doubly-transitive group is the group of affine transformations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380040.png" />, of some field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380041.png" />. Examples of triply-transitive groups are the groups of fractional-linear transformations of the projective line over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380042.png" />, that is, transformations of the form | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380043.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380044.png" /></td> </tr></table> | |
| − | |||
| − | A | + | A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380045.png" />-transitive group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380046.png" /> is said to be strictly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380048.png" />-transitive if only the identity permutation can leave <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380049.png" /> distinct elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380050.png" /> fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups. |
| − | transitive group | ||
| − | is said to be strictly | ||
| − | transitive if only the identity permutation can leave | ||
| − | distinct elements of | ||
| − | fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups. | ||
| − | The finite [[Symmetric group|symmetric group]] | + | The finite [[Symmetric group|symmetric group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380051.png" /> (acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380052.png" />) is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380053.png" />-transitive. The finite [[Alternating group|alternating group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380054.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380055.png" />-transitive. These two series of multiply-transitive groups are the obvious ones. Two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380056.png" />-transitive groups, namely <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380057.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380058.png" />, are known, as well as two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380059.png" />-transitive groups, namely <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380061.png" /> (see [[#References|[3]]] and also [[Mathieu group|Mathieu group]]). There is the conjecture that apart from these four groups there are no non-trivial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380062.png" />-transitive groups for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380063.png" />. This conjecture has been proved, using the classification of finite simple non-Abelian groups [[#References|[6]]]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete. |
| − | acting on | ||
| − | is | ||
| − | transitive. The finite [[Alternating group|alternating group]] | ||
| − | is | ||
| − | transitive. These two series of multiply-transitive groups are the obvious ones. Two | ||
| − | transitive groups, namely | ||
| − | and | ||
| − | are known, as well as two | ||
| − | transitive groups, namely | ||
| − | and | ||
| − | see [[#References|[3]]] and also [[Mathieu group|Mathieu group]]). There is the conjecture that apart from these four groups there are no non-trivial | ||
| − | transitive groups for | ||
| − | This conjecture has been proved, using the classification of finite simple non-Abelian groups [[#References|[6]]]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete. | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380064.png" />-Transitive groups have also been defined for fractional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380065.png" /> of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380067.png" />. Namely, a permutation group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380068.png" /> is said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380069.png" />-transitive if either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380070.png" />, or if all orbits of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380071.png" /> have the same length greater than 1. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380072.png" />, a group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380073.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380074.png" />-transitive if the stabilizer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380075.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380076.png" />-transitive on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380077.png" /> (see [[#References|[3]]]). | |
| − | Transitive groups have also been defined for fractional | ||
| − | of the form | ||
| − | |||
| − | Namely, a permutation group | ||
| − | is said to be | ||
| − | transitive if either | ||
| − | or if all orbits of | ||
| − | have the same length greater than 1. For | ||
| − | a group | ||
| − | is | ||
| − | transitive if the stabilizer | ||
| − | is | ||
| − | transitive on | ||
| − | see [[#References|[3]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Hall, "The theory of groups" , Macmillan (1959)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Passman, "Permutation groups" , Benjamin (1968)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D.G. Higman, "Lecture on permutation representations" , Math. Inst. Univ. Giessen (1977)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> P.J. Cameron, "Finite permutation groups and finite simple groups" ''Bull. London Math. Soc.'' , '''13''' (1981) pp. 1–22</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Hall, "The theory of groups" , Macmillan (1959)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Passman, "Permutation groups" , Benjamin (1968)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D.G. Higman, "Lecture on permutation representations" , Math. Inst. Univ. Giessen (1977)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> P.J. Cameron, "Finite permutation groups and finite simple groups" ''Bull. London Math. Soc.'' , '''13''' (1981) pp. 1–22</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | The degree of a permutation group | + | The degree of a permutation group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380078.png" /> is the number of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380079.png" />. An (abstract) group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380080.png" /> is said to be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380082.png" />-transitive group if it can be realized as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380083.png" />-fold transitive permutation group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380084.png" />. |
| − | is the number of elements of | ||
| − | An (abstract) group | ||
| − | is said to be a | ||
| − | transitive group if it can be realized as a | ||
| − | fold transitive permutation group | ||
| − | Due to the classification of finite simple groups, all | + | Due to the classification of finite simple groups, all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380085.png" />-transitive permutation groups have been found. See the list and references in [[#References|[a1]]]. |
| − | transitive permutation groups have been found. See the list and references in [[#References|[a1]]]. | ||
| − | An important concept for transitive permutation groups is the permutation rank. It can be defined as the number of orbits of | + | An important concept for transitive permutation groups is the permutation rank. It can be defined as the number of orbits of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380086.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380087.png" />. |
| − | on | ||
| − | Primitive permutation groups with permutation rank | + | Primitive permutation groups with permutation rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093800/t09380088.png" /> have been almost fully classified by use of the classification of finite simple groups [[#References|[a2]]]. |
| − | have been almost fully classified by use of the classification of finite simple groups [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Cohen, H. Zantema, "A computation concerning doubly transitive permutation groups" ''J. Reine Angew. Math.'' , '''347''' (1984) pp. 196–211</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance regular graphs" , Springer (1989) pp. 229</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Cohen, H. Zantema, "A computation concerning doubly transitive permutation groups" ''J. Reine Angew. Math.'' , '''347''' (1984) pp. 196–211</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance regular graphs" , Springer (1989) pp. 229</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020
A permutation group 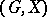 such that each element
such that each element 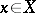 can be taken to any element
can be taken to any element 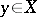 by a suitable element
by a suitable element 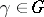 , that is,
, that is, 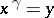 . In other words,
. In other words, 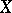 is the unique orbit of the group
is the unique orbit of the group 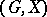 . If the number of orbits is greater than 1, then
. If the number of orbits is greater than 1, then 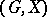 is said to be intransitive. The orbits of an intransitive group are sometimes called its domains of transitivity. For an intransitive group
is said to be intransitive. The orbits of an intransitive group are sometimes called its domains of transitivity. For an intransitive group 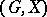 with orbits
with orbits 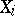 ,
,
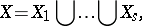 |
and the restriction of the group action to 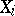 is transitive.
is transitive.
Let 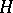 be a subgroup of a group
be a subgroup of a group 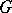 and let
and let
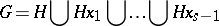 |
be the decomposition of 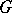 into right cosets with respect to
into right cosets with respect to 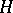 . Further, let
. Further, let 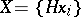 . Then the action of
. Then the action of 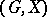 is defined by
is defined by 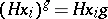 . This action is transitive and, conversely, every transitive action is of the above type for a suitable subgroup
. This action is transitive and, conversely, every transitive action is of the above type for a suitable subgroup 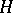 of
of 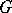 .
.
An action  is said to be
is said to be 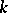 -transitive,
-transitive, 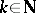 , if for any two ordered sets of
, if for any two ordered sets of 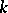 distinct elements
distinct elements 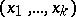 and
and 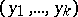 ,
, 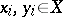 , there exists an element
, there exists an element 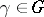 such that
such that 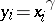 for all
for all 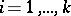 . In other words,
. In other words, 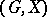 possesses just one anti-reflexive
possesses just one anti-reflexive 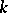 -orbit. For
-orbit. For 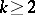 , a
, a 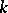 -transitive group is called multiply transitive. An example of a doubly-transitive group is the group of affine transformations
-transitive group is called multiply transitive. An example of a doubly-transitive group is the group of affine transformations  ,
, 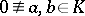 , of some field
, of some field 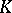 . Examples of triply-transitive groups are the groups of fractional-linear transformations of the projective line over a field
. Examples of triply-transitive groups are the groups of fractional-linear transformations of the projective line over a field 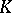 , that is, transformations of the form
, that is, transformations of the form
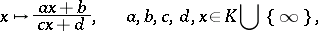 |
where
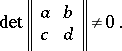 |
A 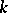 -transitive group
-transitive group  is said to be strictly
is said to be strictly 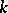 -transitive if only the identity permutation can leave
-transitive if only the identity permutation can leave 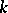 distinct elements of
distinct elements of 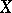 fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups.
fixed. The group of affine transformations and the group of fractional-linear transformations are examples of strictly doubly- and strictly triply-transitive groups.
The finite symmetric group 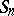 (acting on
(acting on 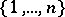 ) is
) is  -transitive. The finite alternating group
-transitive. The finite alternating group 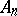 is
is  -transitive. These two series of multiply-transitive groups are the obvious ones. Two
-transitive. These two series of multiply-transitive groups are the obvious ones. Two 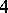 -transitive groups, namely
-transitive groups, namely 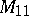 and
and 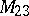 , are known, as well as two
, are known, as well as two  -transitive groups, namely
-transitive groups, namely 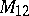 and
and 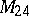 (see [3] and also Mathieu group). There is the conjecture that apart from these four groups there are no non-trivial
(see [3] and also Mathieu group). There is the conjecture that apart from these four groups there are no non-trivial 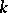 -transitive groups for
-transitive groups for 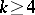 . This conjecture has been proved, using the classification of finite simple non-Abelian groups [6]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete.
. This conjecture has been proved, using the classification of finite simple non-Abelian groups [6]. Furthermore, using the classification of the finite simple groups, the classification of multiply-transitive groups can be considered complete.
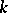 -Transitive groups have also been defined for fractional
-Transitive groups have also been defined for fractional 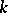 of the form
of the form 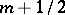 ,
, 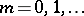 . Namely, a permutation group
. Namely, a permutation group 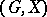 is said to be
is said to be 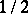 -transitive if either
-transitive if either  , or if all orbits of
, or if all orbits of 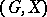 have the same length greater than 1. For
have the same length greater than 1. For 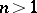 , a group
, a group 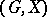 is
is 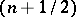 -transitive if the stabilizer
-transitive if the stabilizer 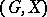 is
is 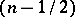 -transitive on
-transitive on 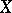 (see [3]).
(see [3]).
References
| [1] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
| [2] | P. Hall, "The theory of groups" , Macmillan (1959) |
| [3] | H. Wielandt, "Finite permutation groups" , Acad. Press (1968) (Translated from German) |
| [4] | D. Passman, "Permutation groups" , Benjamin (1968) |
| [5] | D.G. Higman, "Lecture on permutation representations" , Math. Inst. Univ. Giessen (1977) |
| [6] | P.J. Cameron, "Finite permutation groups and finite simple groups" Bull. London Math. Soc. , 13 (1981) pp. 1–22 |
Comments
The degree of a permutation group  is the number of elements of
is the number of elements of 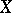 . An (abstract) group
. An (abstract) group 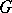 is said to be a
is said to be a 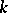 -transitive group if it can be realized as a
-transitive group if it can be realized as a 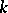 -fold transitive permutation group
-fold transitive permutation group 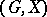 .
.
Due to the classification of finite simple groups, all  -transitive permutation groups have been found. See the list and references in [a1].
-transitive permutation groups have been found. See the list and references in [a1].
An important concept for transitive permutation groups is the permutation rank. It can be defined as the number of orbits of 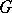 on
on 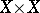 .
.
Primitive permutation groups with permutation rank 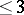 have been almost fully classified by use of the classification of finite simple groups [a2].
have been almost fully classified by use of the classification of finite simple groups [a2].
References
| [a1] | A. Cohen, H. Zantema, "A computation concerning doubly transitive permutation groups" J. Reine Angew. Math. , 347 (1984) pp. 196–211 |
| [a2] | A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance regular graphs" , Springer (1989) pp. 229 |
Transitive group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transitive_group&oldid=49016