Transition with prohibitions
transition with taboo states, for a Markov chain
The set of trajectories of the Markov chain that never enters in a specified set of states in a given time interval. Let, for example,  be a Markov chain with discrete time and set of states
be a Markov chain with discrete time and set of states  , while
, while  is the set of "taboo" states (the taboo set). Then the taboo probabilities
is the set of "taboo" states (the taboo set). Then the taboo probabilities  are
are
 |
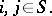 |
The properties of the taboo probabilities  are analogous to those of the ordinary transition probabilities
are analogous to those of the ordinary transition probabilities  , since the families of matrices
, since the families of matrices  and
and  ,
,  , form multiplication semi-groups; however, while
, form multiplication semi-groups; however, while  ,
,  . Different problems, e.g. the study of the distribution of the time to the first entrance of the Markov chain into a given set or limit theorems for branching processes (cf. Branching process) under conditions of non-extinction, in fact amount to the investigation of various properties of taboo probabilities.
. Different problems, e.g. the study of the distribution of the time to the first entrance of the Markov chain into a given set or limit theorems for branching processes (cf. Branching process) under conditions of non-extinction, in fact amount to the investigation of various properties of taboo probabilities.
References
| [1] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960) |
Comments
References
| [a1] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1975) (Translated from Russian) |
Transition with prohibitions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transition_with_prohibitions&oldid=11935