Transition probabilities
The probabilities of transition of a Markov chain  from a state
from a state 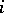 into a state
into a state 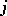 in a time interval
in a time interval 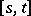 :
:
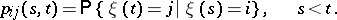 |
In view of the basic property of a Markov chain, for any states 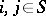 (where
(where 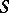 is the set of all states of the chain) and any
is the set of all states of the chain) and any  ,
,
 |
One usually considers homogeneous Markov chains, for which the transition probabilities 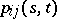 depend on the length of
depend on the length of 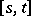 but not on its position on the time axis:
but not on its position on the time axis:
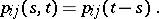 |
For any states 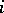 and
and 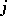 of a homogeneous Markov chain with discrete time, the sequence
of a homogeneous Markov chain with discrete time, the sequence 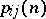 has a Cesàro limit, i.e.
has a Cesàro limit, i.e.
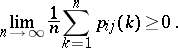 |
Subject to certain additional conditions (and also for chains with continuous time), the limit exists also in the usual sense. See Markov chain, ergodic; Markov chain, class of positive states of a.
The transition probabilities 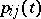 for a Markov chain with discrete time are determined by the values of
for a Markov chain with discrete time are determined by the values of 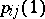 ,
, 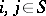 ; for any
; for any 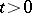 ,
, 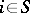 ,
,
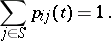 |
In the case of Markov chains with continuous time it is usually assumed that the transition probabilities satisfy the following additional conditions: All the 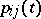 are measurable as functions of
are measurable as functions of 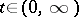 ,
,
 |
Under these assumptions the following transition rates exist:
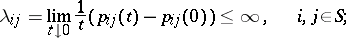 | (1) |
if all the 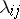 are finite and if
are finite and if 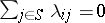 ,
, 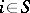 , then the
, then the 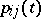 satisfy the Kolmogorov–Chapman system of differential equations
satisfy the Kolmogorov–Chapman system of differential equations
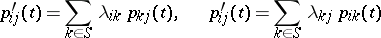 | (2) |
with the initial conditions 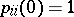 ,
, 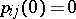 ,
, 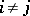 ,
, 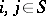 (see also Kolmogorov equation; Kolmogorov–Chapman equation).
(see also Kolmogorov equation; Kolmogorov–Chapman equation).
If a Markov chain is specified by means of the transition rates (1), then the transition probabilities 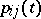 satisfy the conditions
satisfy the conditions
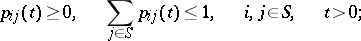 |
chains for which 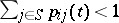 for certain
for certain 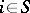 and
and 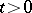 are called defective (in this case the solution to (2) is not unique); if
are called defective (in this case the solution to (2) is not unique); if 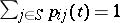 for all
for all 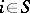 and
and  , the chain is called proper.
, the chain is called proper.
Example. The Markov chain 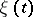 with set of states
with set of states 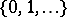 and transition densities
and transition densities
 |
(i.e., a pure birth process) is defective if and only if
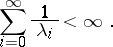 |
Let
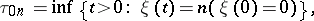 |
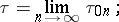 |
then
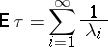 |
and for 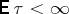 one has
one has 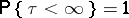 , i.e. the path of
, i.e. the path of 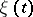 "tends to infinity in a finite time with probability 1" (see also Branching processes, regularity of).
"tends to infinity in a finite time with probability 1" (see also Branching processes, regularity of).
References
| [1] | K.L. Chung, "Markov chains with stationary probability densities" , Springer (1967) |
Comments
For additional references see also Markov chain; Markov process.
In (1), 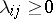 if
if 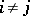 and
and 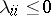 .
.
References
| [a1] | M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980) |
| [a2] | D. Revuz, "Markov chains" , North-Holland (1984) |
Transition probabilities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transition_probabilities&oldid=12319