Transformation group
A permutation group  acting on a set
acting on a set 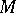 . If, moreover,
. If, moreover,  is endowed with a certain structure and if the elements of
is endowed with a certain structure and if the elements of  preserve this structure, then one appropriately says that
preserve this structure, then one appropriately says that  is a transformation group of this structure. The name of the transformation group reflects to a certain extent the name of the structure endowed on
is a transformation group of this structure. The name of the transformation group reflects to a certain extent the name of the structure endowed on  . E.g. if
. E.g. if  is a vector space over a skew-field, then groups preserving this structure are called linear groups (cf. Linear group). Moreover, automorphism groups of modules over various rings are often called linear groups. In particular, if
is a vector space over a skew-field, then groups preserving this structure are called linear groups (cf. Linear group). Moreover, automorphism groups of modules over various rings are often called linear groups. In particular, if  is a free finite-dimensional module over the ring
is a free finite-dimensional module over the ring  of integers, one speaks of crystallographic groups (cf. Crystallographic group). If
of integers, one speaks of crystallographic groups (cf. Crystallographic group). If 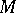 is a topological space and
is a topological space and 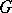 consists of the automorphisms of
consists of the automorphisms of  , one speaks of continuous transformation groups. If
, one speaks of continuous transformation groups. If 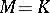 is a field and
is a field and 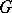 is a finite automorphism group of
is a finite automorphism group of  , then
, then  is the Galois group of the extension
is the Galois group of the extension 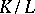 , where
, where 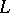 is the subfield of elements that are fixed under the action by elements of
is the subfield of elements that are fixed under the action by elements of 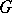 . One can also consider situations in which
. One can also consider situations in which 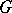 and
and 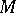 are endowed with structures of the same type and where the action of
are endowed with structures of the same type and where the action of  on
on  is a morphism in the corresponding category. E.g. if
is a morphism in the corresponding category. E.g. if 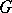 is a topological group continuously acting on a topological space
is a topological group continuously acting on a topological space  , one speaks of a topological transformation group (cf. Topological group); Lie transformation groups and algebraic transformation groups are defined similarly (cf. Lie transformation group; Algebraic group of transformations).
, one speaks of a topological transformation group (cf. Topological group); Lie transformation groups and algebraic transformation groups are defined similarly (cf. Lie transformation group; Algebraic group of transformations).
References
| [1] | A.I. [A.I. Mal'tsev] Mal'cev, "Groups and other algebraic systems" A.D. Aleksandrov (ed.) A.N. Kolmogorov (ed.) M.A. Lavrent'ev (ed.) , Mathematics, its content, methods and meaning , 3 , Amer. Math. Soc. (1962) pp. Chapt. 20 (Translated from Russian) |
Transformation group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transformation_group&oldid=32833