Transcendental number
A number that is not a root of any polynomial with integer coefficients. The domain of definition of such numbers is the field of either the real, complex or 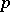 -adic numbers. The existence and explicit construction of transcendental numbers was provided by J. Liouville [1] on the basis of the following fact, noted by him. Irrational algebraic numbers do not have "very good" approximations by rational numbers (see Liouville theorems). Similar considerations enable one to construct
-adic numbers. The existence and explicit construction of transcendental numbers was provided by J. Liouville [1] on the basis of the following fact, noted by him. Irrational algebraic numbers do not have "very good" approximations by rational numbers (see Liouville theorems). Similar considerations enable one to construct 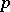 -adic transcendental numbers. G. Cantor [2], after discovering the countability of the set of all algebraic numbers and the uncountability of the set of all real numbers, thus proved that the transcendental real numbers form a set of the cardinality of the continuum. E. Borel [3], after introducing the first concepts of measure theory, established that "almost all" real numbers are transcendental. It was later found that Liouville transcendental numbers form an everywhere-dense subset of the real axis, having the cardinality of the continuum and zero Lebesgue measure. Despite the fact that already in the middle of the 18th century there arose the conjecture on the transcendency of numbers such as
-adic transcendental numbers. G. Cantor [2], after discovering the countability of the set of all algebraic numbers and the uncountability of the set of all real numbers, thus proved that the transcendental real numbers form a set of the cardinality of the continuum. E. Borel [3], after introducing the first concepts of measure theory, established that "almost all" real numbers are transcendental. It was later found that Liouville transcendental numbers form an everywhere-dense subset of the real axis, having the cardinality of the continuum and zero Lebesgue measure. Despite the fact that already in the middle of the 18th century there arose the conjecture on the transcendency of numbers such as  ,
, 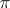 ,
, 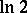 ,
, 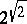 , etc., proofs of this could not be obtained. The transcendency of
, etc., proofs of this could not be obtained. The transcendency of  was proved by Ch. Hermite [4], that of
was proved by Ch. Hermite [4], that of 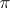 and, more generally, of logarithms of algebraic numbers by C.L.F. Lindemann [5], that of
and, more generally, of logarithms of algebraic numbers by C.L.F. Lindemann [5], that of  by A.O. Gel'fond [6]; C.L. Siegel [7] developed a general method for proving transcendency and algebraic independence of the values at algebraic points of entire functions of a specific class (the
by A.O. Gel'fond [6]; C.L. Siegel [7] developed a general method for proving transcendency and algebraic independence of the values at algebraic points of entire functions of a specific class (the 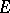 -functions), satisfying a linear differential equation with polynomial coefficients (cf. Siegel method). Gel'fond [8] and T. Schneider [9] simultaneously and independently proved that
-functions), satisfying a linear differential equation with polynomial coefficients (cf. Siegel method). Gel'fond [8] and T. Schneider [9] simultaneously and independently proved that  is transcendental if
is transcendental if  is algebraic and
is algebraic and 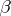 is an algebraic irrational (the so-called Hilbert's seventh problem); A. Baker [10] proved the transcendency of products of numbers of the form
is an algebraic irrational (the so-called Hilbert's seventh problem); A. Baker [10] proved the transcendency of products of numbers of the form 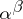 under natural restrictions. Similar results have been obtained for
under natural restrictions. Similar results have been obtained for  -adic transcendental numbers (including Engel's theory of
-adic transcendental numbers (including Engel's theory of 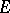 -functions). The development of methods of the theory of transcendental numbers has proved to have a strong influence on new studies in Diophantine equations [10], [11].
-functions). The development of methods of the theory of transcendental numbers has proved to have a strong influence on new studies in Diophantine equations [10], [11].
References
| [1] | J. Liouville, "Sur des classes de très étendues de quantités dont la valeur n'est ni algébrique, ni même réductible à des irrationelles algébriques" C.R. Acad. Sci. , 18 (1844) pp. 883–885; 910–911 |
| [2] | G. Cantor, "Gesammelte Abhandlungen mathematischen und philosophischen Inhalts" , G. Olms, reprint (1962) |
| [3] | E. Borel, "Leçons sur les fonctions discontinues" , Gauthier-Villars (1898) |
| [4] | Ch. Hermite, "Sur la fonction exponentielle" C.R. Acad. Sci. , 77 (1873) pp. 18–24; 74–79; 221–233; 285–293 |
| [5] | C.L.F. Lindemann, "Ueber die Zahl  " Math. Ann. , 20 (1882) pp. 213–225 " Math. Ann. , 20 (1882) pp. 213–225 |
| [6] | A.O. Gel'fond, "Sur les nombre transcendants" C.R. Acad. Sci. , 189 (1929) pp. 1224–1226 |
| [7] | C.L. Siegel, "Ueber einige Anwendungen diophantischer Approximationen" Abhandl. Preuss. Akad. Wiss., Phys. Kl. , 1 (1929) pp. 1–70 |
| [8] | A.O. Gel'fond, "Sur le septième problème de Hilbert" Dokl. Akad. Nauk SSSR , 2 (1934) pp. 4–6 |
| [9] | T. Schneider, "Transzendenzuntersuchungen periodischer Functionen I, II" J. Reine Angew. Math. , 172 (1934) pp. 65–69; 70–74 |
| [10] | A. Baker, "Transcendental number theory" , Cambridge Univ. Press (1975) |
| [11] | V.G. Sprindzhuk, "Classical Diophantine equations in two unknowns" , Moscow (1982) (In Russian) |
| [12] | N.I. Fel'dman, "Hilbert's seventh problem" , Moscow (1982) (In Russian) |
Comments
The results of Gel'fond and Schneider imply that for any 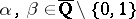 ,
, 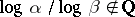 implies
implies 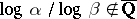 . Baker's generalization asserts that for any
. Baker's generalization asserts that for any  ,
,  -linear independence of
-linear independence of 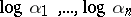 implies
implies 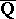 -linear independence of
-linear independence of 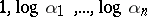 . Moreover, one can give effective lower bounds for such linear forms. This has profound consequences for the theory of Diophantine equations (see [10]). Gel'fond's and Schneider's method has been further generalized to include
. Moreover, one can give effective lower bounds for such linear forms. This has profound consequences for the theory of Diophantine equations (see [10]). Gel'fond's and Schneider's method has been further generalized to include  -linear independence of periods and quasi-periods of elliptic curves and finally, through the work of G. Wüstholz, P. Philippon and M. Waldschmidt, this has resulted into very general statements of
-linear independence of periods and quasi-periods of elliptic curves and finally, through the work of G. Wüstholz, P. Philippon and M. Waldschmidt, this has resulted into very general statements of 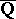 -linear independence on commutative algebraic groups defined over
-linear independence on commutative algebraic groups defined over 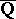 .
.
References
| [a1] | K. Mahler, "Lectures on transcendental numbers" , Lect. notes in math. , 546 , Springer (1976) |
| [a2] | A.O. Gel'fond, "Transcendental and algebraic numbers" , Dover, reprint (1960) (Translated from Russian) |
| [a3] | D., et al. Bertrand, "Les nombres transcendants" Mem. Soc. Math. France , 13 (1984) |
| [a4] | A.B. Shidlovskii, "Transcendental numbers" , de Gruyter (1989) (Translated from Russian) |
| [a5] | Y. André, "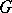 -functions and geometry" , Vieweg (1988) -functions and geometry" , Vieweg (1988) |
Transcendental number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_number&oldid=13628