Transcendental extension

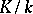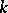A field extension that is not algebraic (cf. Extension of a field). An extension is transcendental if and only if the field contains elements that are transcendental over , that is, elements that are not roots of any non-zero polynomial with coefficients in .

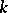The elements of a set are called algebraically independent over 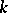if for any finite set 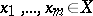and any non-zero polynomial with coefficients in ,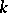

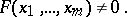The elements of 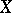are transcendental over 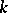. If is a maximal set of algebraically independent elements over , then 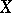is called a transcendence basis of 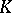over 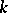. The cardinality of is called the transcendence degree of over 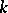and is an invariant of the extension 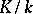. For a tower of fields 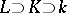, the transcendence degree of 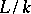is equal to the sum of the transcendence degrees of 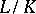and .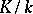

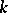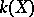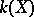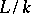If all elements of a set are algebraically independent over , then the extension is called purely transcendental. In this case the field is isomorphic to the field of rational functions in the set of variables over . Any field extension can be represented as a tower of extensions , where 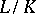is an algebraic and 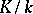is a purely transcendental extension. If 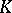can be chosen so that 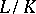is a separable extension, then the extension 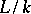is called separably generated, and the transcendence basis of over 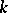is called a separating basis. If is separably generated over 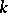, then 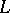is separable over 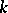. In the case when the extension 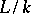is finitely generated, the converse holds as well. By definition, an extension is separable if and only if any derivation (cf. Derivation in a ring) of extends to 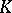. Such an extension is uniquely determined for any derivation if and only if the extension is algebraic.

References

[1]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975)
[2]	N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Springer (1988) pp. Chapt. 4–6 (Translated from French)

Comments

The Noether normalization lemma says that if 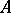is an integral domain that is finitely generated as a ring over a field 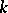, then there exist 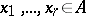that are algebraically independent over 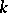such that 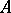is integral over .

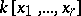References

[a1]	P.M. Cohn, "Algebra" , 1–2 , Wiley (1989) pp. Vol. 2, 350; Vol. 3, 168ff