Trace on a C*-algebra
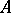
An additive functional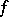 
on the set 
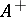of positive elements of 
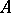that takes values in 
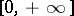, is homogeneous with respect to multiplication by positive numbers and satisfies the condition 
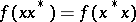for all 
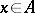. A trace 
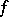is said to be finite if 
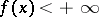for all 
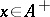, and semi-finite if 
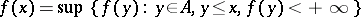for all 
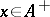. The finite traces on 
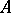are the restrictions to 
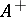of those positive linear functionals 
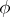on 
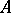such that 
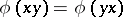for all 
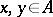. Let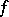 
be a trace on 
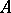, let 
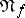be the set of elements 
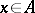such that 
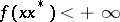, and let 
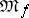be the set of linear combinations of products of pairs of elements of 
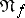. Then 
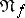and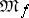 
are self-adjoint two-sided ideals of 
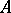, and there is a unique linear functional 
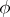on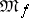 
that coincides with 
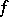on 
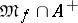. Let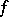 
be a lower semi-continuous semi-finite trace on a 
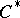-algebra 
. Then the formula 
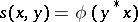defines a Hermitian form on 
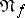, with respect to which the mapping 
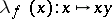of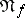 
into itself is continuous for any 
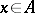. Put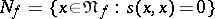 
, and let 
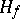be the completion of the quotient space 
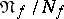with respect to the scalar product defined by the form 
. By passing to the quotient space and subsequent completion, the operators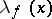 
determine certain operators 
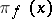on the Hilbert space 
, and the mapping 
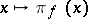is a representation of the 
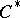-algebra 
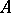in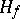 
. The mapping 
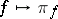establishes a one-to-one correspondence between the set of lower semi-continuous semi-finite traces on 
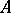and the set of representations of 
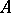with a trace, defined up to quasi-equivalence.
References
| [1] | J. Dixmier, " algebras" , North-Holland (1977) (Translated from French) |
Comments
Cf. also 
-algebra; Trace; Quasi-equivalent representations.
References
| [a1] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) |
Trace on a C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trace_on_a_C*-algebra&oldid=16757