Tournament
An oriented graph (cf. also Graph, oriented) without loops, each pair of vertices of which are joined by an arc in exactly one direction. A tournament with  vertices can be regarded as the outcome of a competition with
vertices can be regarded as the outcome of a competition with  players, the rules of which forbid draws. The notion of a tournament is used for ordering
players, the rules of which forbid draws. The notion of a tournament is used for ordering  objects by the method of pairwise comparison. In this connection it finds application in biology, sociology, etc.
objects by the method of pairwise comparison. In this connection it finds application in biology, sociology, etc.
A tournament is said to be transitive if its vertices can be indexed by the numbers 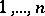 in such a way that there is an arc going from
in such a way that there is an arc going from 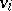 to
to 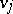 if and only if
if and only if 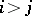 . There are no circuits in a transitive tournament. A tournament is said to be strong if for any ordered pair of vertices
. There are no circuits in a transitive tournament. A tournament is said to be strong if for any ordered pair of vertices 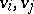 there exists a directed path from
there exists a directed path from 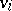 to
to 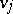 . A set of arcs in a tournament is called compatible if there are no circuits in the subgraph formed by these arcs and the vertices incident to them. The maximum cardinality of a set of compatible arcs is a measure of compatibility in the definition of "the winner" of the tournament. Every tournament contains a subset of compatible arcs of cardinality not less than
. A set of arcs in a tournament is called compatible if there are no circuits in the subgraph formed by these arcs and the vertices incident to them. The maximum cardinality of a set of compatible arcs is a measure of compatibility in the definition of "the winner" of the tournament. Every tournament contains a subset of compatible arcs of cardinality not less than 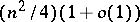 . Another measure of compatibility is the ratio of the number of transitive
. Another measure of compatibility is the ratio of the number of transitive 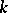 -vertex subtournaments of a tournament with
-vertex subtournaments of a tournament with  vertices to the number of strong
vertices to the number of strong 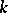 -vertex subtournaments. The maximum number of strong
-vertex subtournaments. The maximum number of strong 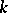 -vertex subtournaments of a tournament with
-vertex subtournaments of a tournament with  vertices is equal to
vertices is equal to
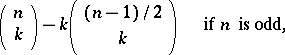 |
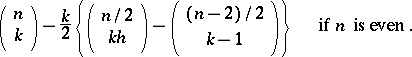 |
A tournament is strong if and only if it has a spanning cycle (Hamiltonian circuit). Every strong tournament with  vertices has a circuit of length
vertices has a circuit of length 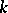 for
for 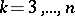 . Every tournament has a spanning path (Hamiltonian path).
. Every tournament has a spanning path (Hamiltonian path).
The outdegrees 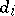 of a tournament with
of a tournament with  vertices satisfy the equation
vertices satisfy the equation
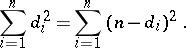 |
Suppose that a set of integers 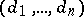 satisfies the condition
satisfies the condition 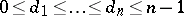 . Then a tournament with outdegrees
. Then a tournament with outdegrees 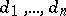 exists if and only if for any
exists if and only if for any  the inequality
the inequality
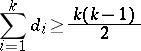 |
holds, with equality for 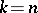 . Furthermore, a tournament is strong if and only if
. Furthermore, a tournament is strong if and only if
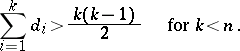 |
If 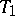 and
and 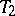 are two subtournaments of a tournament
are two subtournaments of a tournament 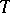 and if there exists an arc
and if there exists an arc 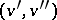 for each pair of vertices
for each pair of vertices 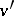 in
in 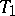 and
and 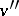 in
in 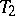 , then one writes
, then one writes 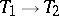 . Suppose that the set of vertices of a tournament is partitioned into non-intersecting subsets
. Suppose that the set of vertices of a tournament is partitioned into non-intersecting subsets 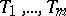 . Suppose further that either
. Suppose further that either 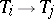 or
or  for
for 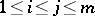 . Then the partition defines an equivalence relation on the vertices of
. Then the partition defines an equivalence relation on the vertices of 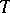 . A tournament is called simple if no non-trivial equivalence relation can be defined on its vertices. Every tournament with
. A tournament is called simple if no non-trivial equivalence relation can be defined on its vertices. Every tournament with  vertices is a subtournament of some simple tournament with
vertices is a subtournament of some simple tournament with 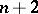 vertices. A tournament
vertices. A tournament 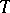 with
with  vertices is a subtournament of some simple tournament with
vertices is a subtournament of some simple tournament with 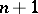 vertices if and only if
vertices if and only if 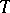 is neither a circuit with three vertices nor a non-trivial transitive tournament with an odd number of vertices. The number of pairwise non-isomorphic tournaments with
is neither a circuit with three vertices nor a non-trivial transitive tournament with an odd number of vertices. The number of pairwise non-isomorphic tournaments with  vertices is asymptotically equal to
vertices is asymptotically equal to
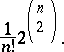 |
The number of distinct tournaments with  indexed vertices is equal to
indexed vertices is equal to
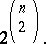 |
The generating functions 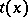 and
and 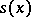 for tournaments and strong tournaments, respectively, are related by the formula:
for tournaments and strong tournaments, respectively, are related by the formula:
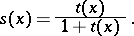 |
Every tournament with  vertices,
vertices, 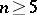 , that is not strong is uniquely recoverable from the family of its
, that is not strong is uniquely recoverable from the family of its 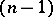 -vertex subtournaments.
-vertex subtournaments.
References
| [1] | F. Harary, "Graph theory" , Addison-Wesley (1969) pp. Chapt. 9 |
| [2] | J.W. Moon, "Topics on tournaments" , Holt, Rinehart & Winston (1968) |
Comments
A random tournament over 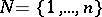 is defined by making random choices of an arc
is defined by making random choices of an arc 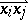 or
or 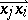 for each pair of different vertices
for each pair of different vertices 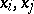 , the choice being equiprobable and independent for all different pairs. Cf. [2] for many results on random tournaments.
, the choice being equiprobable and independent for all different pairs. Cf. [2] for many results on random tournaments.
References
| [a1] | F. Harary, L. Moser, "The theory of round robin tournaments" Amer. Math. Monthly , 73 (1966) pp. 231–246 |
| [a2] | L. Comtet, "Advanced combinatorics" , Reidel (1974) pp. 68ff (Translated from French) |
Tournament. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tournament&oldid=11816