Totient function
Euler totient function, Euler totient
Another frequently used named for the Euler function  , which counts the natural numbers
, which counts the natural numbers 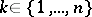 that are relatively prime to
that are relatively prime to  .
.
The Carmichael conjecture on the Euler totient function states that if 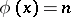 , then
, then 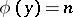 for some
for some  ; i.e. no value of the Euler function is assumed once. This has now been verified for
; i.e. no value of the Euler function is assumed once. This has now been verified for 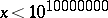 , [a1].
, [a1].
A natural generalization of the Euler totient function is the Jordan totient function 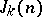 , which counts the number of
, which counts the number of 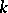 -tuples
-tuples 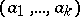 ,
, 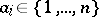 , such that
, such that  . Clearly,
. Clearly, 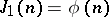 .
.
One has
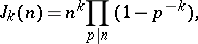 |
where 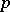 runs over the prime numbers dividing
runs over the prime numbers dividing  , and
, and
 |
where 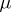 is the Möbius function and
is the Möbius function and 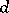 runs over all divisors of
runs over all divisors of  . For
. For  these formulas reduce to the well-known formulas for the Euler function.
these formulas reduce to the well-known formulas for the Euler function.
The Lehmer problem on the Euler totient function asks for the solutions of 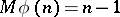 ,
,  , [a2]. For some results on this still (1996) largely open problem, see [a3] and the references therein. The corresponding problem for the Jordan totient function (and
, [a2]. For some results on this still (1996) largely open problem, see [a3] and the references therein. The corresponding problem for the Jordan totient function (and 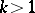 ) is easy, [a4]: For
) is easy, [a4]: For  ,
, 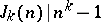 if and only if
if and only if  is a prime number. Moreover, if
is a prime number. Moreover, if  is a prime number, then
is a prime number, then 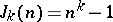 .
.
For much more information on the Euler totient function, the Jordan totient function and various other generalizations, see [a5], [a6].
References
| [a1] | A. Schlafly, S. Wagon, "Carmichael's conjecture on the Euler function is valid below 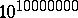 " Math. Comp. , 63 (1994) pp. 415–419 " Math. Comp. , 63 (1994) pp. 415–419 |
| [a2] | D.H. Lehmer, "On Euler's totient function" Bull. Amer. Math. Soc. , 38 (1932) pp. 745–751 |
| [a3] | V. Siva Rama Prasad, M. Rangamma, "On composite  for which for which  " Nieuw Archief voor Wiskunde (4) , 5 (1987) pp. 77–83 " Nieuw Archief voor Wiskunde (4) , 5 (1987) pp. 77–83 |
| [a4] | M.V. Subbarao, V. Siva Rama Prasad, "Some analogues of a Lehmer problem on the totient function" Rocky Mount. J. Math. , 15 (1985) pp. 609–620 |
| [a5] | R. Sivamarakrishnan, "The many facets of Euler's totient II: generalizations and analogues" Nieuw Archief Wiskunde (4) , 8 (1990) pp. 169–188 |
| [a6] | R. Sivamarakrishnan, "The many facets of Euler's totient I" Nieuw Archief Wiskunde (4) , 4 (1986) pp. 175–190 |
| [a7] | L.E. Dickson, "History of the theory of numbers" , I: Divisibility and primality , Chelsea, reprint (1971) pp. Chapt. V; 113–155 |
Totient function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totient_function&oldid=12673