Totally-geodesic manifold
From Encyclopedia of Mathematics
totally-geodesic submanifold
A submanifold 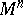 of a Riemannian space
of a Riemannian space 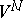 such that the geodesic lines (cf. Geodesic line) of
such that the geodesic lines (cf. Geodesic line) of 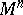 are also geodesic lines in
are also geodesic lines in 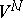 . A totally-geodesic submanifold is characterized by the fact that for every normal vector of
. A totally-geodesic submanifold is characterized by the fact that for every normal vector of 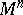 the corresponding second fundamental form vanishes; this is equivalent to the vanishing of all normal curvatures of
the corresponding second fundamental form vanishes; this is equivalent to the vanishing of all normal curvatures of 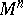 .
.
Comments
The existence of totally-geodesic submanifolds in a general Riemannian manifold is exceptional. Conversely, the existence of many such totally-geodesic submanifolds is used in various recent work to characterize some special manifolds, e.g. symmetric spaces. See [a1].
References
| [a1] | W. Ballmann, M. Gromov, V. Schroeder, "Manifolds of non-positive curvature" , Birkhäuser (1985) |
| [a2] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) |
How to Cite This Entry:
Totally-geodesic manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-geodesic_manifold&oldid=13471
Totally-geodesic manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-geodesic_manifold&oldid=13471
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article