Totally-disconnected space
A space in which any subset containing more than one point is disconnected. An equivalent condition is that the connected component of any point in the space is that point itself. The topological product and the topological sum of totally-disconnected spaces, as well as any subspace of a totally-disconnected space, are totally disconnected. Any totally-disconnected compactum is zero-dimensional (in every sense). Such compacta are important, in particular, because they are Stone spaces of Boolean algebras. A totally-disconnected space (a Knaster–Kuratowski fan) in the plane that can be made into a connected space as a result of the addition of a single point, has been constructed. Such a space is not zero-dimensional. In a Hilbert space, the subspace formed by the points all coordinates of which are rational is totally disconnected and one-dimensional. If each point in a space is the intersection of all closed-and-open sets including it, the space is totally disconnected (in particular, all zero-dimensional spaces are totally disconnected). However, there exists a totally-disconnected metric space with a countable base in which not all points are intersections of such closed-and-open sets.
References
| [1] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
| [2] | R. Engelking, "Outline of general topology" , North-Holland (1968) (Translated from Polish) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
| [4] | N. Bourbaki, "Elements of mathematics. General topology" , Springer (1989) (Translated from French) |
Comments
There is a totally-disconnected plane set  , no proper superset of which is totally disconnected, [a3]. The complement of such a set is called a primitive dispersion set for the plane. For all
, no proper superset of which is totally disconnected, [a3]. The complement of such a set is called a primitive dispersion set for the plane. For all  , there are
, there are  -dimensional totally-disconnected separable metric groups, [a4].
-dimensional totally-disconnected separable metric groups, [a4].
There is some confusion in the terminology concerning disconnected spaces. There are a few kinds of disconnectedness; the two most common notions are: i) the one in the article: connected subsets consist of at most one point; and ii) for every two points  and
and  there is a closed-and-open set
there is a closed-and-open set  such that
such that  and
and  .
.
Both are called total disconnectedness at times. References [a1] and [a2] call spaces satisfying ii) totally disconnected, and in [a2] spaces satisfying i) are called hereditarily disconnected (because they have no non-trivial connected subspaces). (Note that ii) implies i).)
The Knaster–Kuratowski fan is a subset of the plane defined as follows: Consider the usual Cantor middle-third set  situated in the interval
situated in the interval 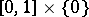 in the plane. Connect every point
in the plane. Connect every point  of
of  with the point
with the point 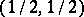 by the line segment
by the line segment 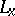 . For each
. For each 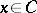 take a subset
take a subset  of
of 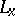 as follows: if
as follows: if  is an end-point of an interval in the complement of
is an end-point of an interval in the complement of 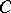 take all points of
take all points of  with rational second coordinate, otherwise take the points with irrational second coordinate. The union
with rational second coordinate, otherwise take the points with irrational second coordinate. The union 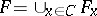 is the Knaster–Kuratowksi fan. When one removes the point
is the Knaster–Kuratowksi fan. When one removes the point  from
from 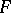 , one obtains a space that satisfies i) above but not ii). See also Kuratowski–Knaster fan.
, one obtains a space that satisfies i) above but not ii). See also Kuratowski–Knaster fan.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [a2] | R. Engelking, "General topology" , Heldermann (1989) |
| [a3] | M.E. Estill, "A primitive dispersion set of the plane" Duke Math. J. , 9 : 19 (1952) (323–328) |
| [a4] | J. van Mill, " -dimensional totally disconnected topological groups" Math. Japon. , 32 (1987) pp. 267–273 -dimensional totally disconnected topological groups" Math. Japon. , 32 (1987) pp. 267–273 |
Totally-disconnected space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-disconnected_space&oldid=17994