Total variation of a function
From Encyclopedia of Mathematics
The same as the variation of a function of one variable. The total variation of a real-valued function is the sum of its positive variation (cf. Positive variation of a function) and negative variation (cf. Negative variation of a function).
Comments
If  is a complex-valued function on
is a complex-valued function on  , then its total variation over
, then its total variation over  is the number
is the number
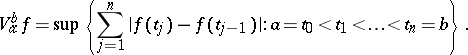 |
If  is also continuous, then this number is the same as the length of the arc in the complex plane that is parametrized by
is also continuous, then this number is the same as the length of the arc in the complex plane that is parametrized by  . If
. If 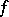 is absolutely continuous on
is absolutely continuous on  , then
, then
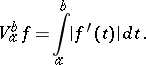 |
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
How to Cite This Entry:
Total variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Total_variation_of_a_function&oldid=28014
Total variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Total_variation_of_a_function&oldid=28014
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article