Torsion tensor
From Encyclopedia of Mathematics
A tensor of type 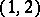 that is skew-symmetric with respect to its indices, obtained by decomposing the torsion form of a connection in terms of a local cobasis on a manifold
that is skew-symmetric with respect to its indices, obtained by decomposing the torsion form of a connection in terms of a local cobasis on a manifold 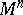 . In particular, in terms of a holonomic cobasis
. In particular, in terms of a holonomic cobasis 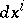 ,
, 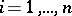 , the components
, the components 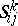 of the torsion tensor are expressed in terms of the Christoffel symbols (cf. Christoffel symbol)
of the torsion tensor are expressed in terms of the Christoffel symbols (cf. Christoffel symbol) 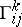 of the connection as follows:
of the connection as follows:
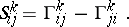 |
Comments
In terms of covariant derivatives  and vector fields
and vector fields 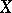 ,
, 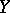 the torsion tensor
the torsion tensor 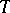 can be described as follows:
can be described as follows:
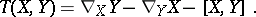 |
References
| [a1] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
| [a2] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [a3] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
How to Cite This Entry:
Torsion tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion_tensor&oldid=49000
Torsion tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion_tensor&oldid=49000
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article