Topological transitivity
A property defined for a topological dynamical system 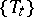 , usually for a flow or a cascade (the time
, usually for a flow or a cascade (the time 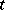 runs through the real numbers or the integers). It consists of the existence of a trajectory
runs through the real numbers or the integers). It consists of the existence of a trajectory 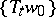 that has the whole phase space
that has the whole phase space 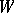 as its
as its 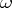 -limit set. (Cf. Limit set of a trajectory; an equivalent condition is the existence of a positive semi-trajectory
-limit set. (Cf. Limit set of a trajectory; an equivalent condition is the existence of a positive semi-trajectory 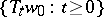 that is everywhere dense in
that is everywhere dense in 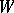 .) Such a trajectory (semi-trajectory) is called topologically transitive.
.) Such a trajectory (semi-trajectory) is called topologically transitive.
Closely related to topological transitivity is the property of transitivity of domains: For any non-empty open sets 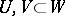 there is a
there is a 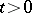 such that
such that 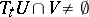 . More precisely, topological transitivity implies transitivity of domains, and the converse holds (cf. [1], [2]) if
. More precisely, topological transitivity implies transitivity of domains, and the converse holds (cf. [1], [2]) if 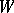 is a complete separable metric space (in this case the set of topologically-transitive trajectories has the cardinality of the continuum). Hence, with the same hypotheses on
is a complete separable metric space (in this case the set of topologically-transitive trajectories has the cardinality of the continuum). Hence, with the same hypotheses on  , the property of topological transitivity is symmetric with respect to the time direction: If there exists a trajectory
, the property of topological transitivity is symmetric with respect to the time direction: If there exists a trajectory 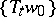 having the whole of
having the whole of 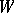 as its
as its 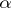 -limit set, then one has transitivity of domains and topological transitivity.
-limit set, then one has transitivity of domains and topological transitivity.
Often topological transitivity is used to mean the existence of a trajectory 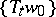 that is everywhere dense in
that is everywhere dense in 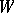 . (The difference between the definitions is essential when the points of this trajectory form an open set in
. (The difference between the definitions is essential when the points of this trajectory form an open set in 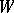 ; otherwise it is itself an
; otherwise it is itself an 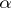 -limit or
-limit or 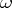 -limit, and hence the whole of
-limit, and hence the whole of 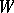 is its
is its 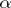 -limit or
-limit or 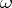 -limit set.) The last definition is also used for more general transformation groups [3]. The definition and some of the results also carry over to the case of non-invertible mappings and semi-groups, although one is usually not concerned with these in topological dynamics.
-limit set.) The last definition is also used for more general transformation groups [3]. The definition and some of the results also carry over to the case of non-invertible mappings and semi-groups, although one is usually not concerned with these in topological dynamics.
References
| [1] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) |
Comments
A topological dynamical system with the property of transitivity of domains is also called topological ergodic (in [3] it is called regionally transitive). In many cases, topological transitivity is implied by metric transitivity.
Topological transitivity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_transitivity&oldid=13191