Topological semi-group
A set equipped with both the algebraic structure of a semi-group and the structure of a topological Hausdorff space, such that the semi-group operation is continuous in the given topology. Any semi-group is a topological semi-group in the discrete topology. There exist semi-groups which admit only the discrete topology. Any Hausdorff space can be made into a topological semi-group, e.g. by giving it a left-singular or zero multiplication.
Several independent branches of topological semi-groups have emerged: the general theory of compact semi-groups (cf. Compactness); homotopy properties of topological semi-groups; the study of semi-groups on concrete topological spaces; harmonic analysis on topological semi-groups; and semi-groups of continuous transformations of topological spaces. Besides, the study of topological semi-groups began in connection with the consideration of all closed sub-semi-groups.
A natural class of topological semi-groups, which includes the compact and discrete semi-groups, is that of the locally compact semi-groups. However, many properties which hold for compact and discrete semi-groups cease to hold for arbitrary locally compact semi-groups. Hence one usually imposes additional restrictions of algebraic or topological character. An important condition of this type is weak uniformity: A locally compact semi-group 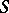 is called weakly uniform if, for any
is called weakly uniform if, for any 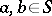 (one of these elements may be the empty symbol) and any subsets
(one of these elements may be the empty symbol) and any subsets 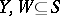 , where
, where 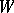 is an open subset with compact closure
is an open subset with compact closure 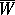 and
and 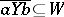 or
or 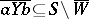 , there exist neighbourhoods
, there exist neighbourhoods 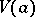 and
and 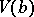 of
of  and
and 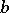 such that
such that 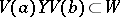 , respectively
, respectively 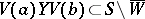 . The class of weakly-uniform semi-groups contains all compact semi-groups, discrete semi-groups and locally compact groups. If a locally compact semi-group
. The class of weakly-uniform semi-groups contains all compact semi-groups, discrete semi-groups and locally compact groups. If a locally compact semi-group 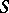 is a group, then the mapping of taking the inverse is continuous, i.e.
is a group, then the mapping of taking the inverse is continuous, i.e. 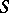 is a topological group. In a locally compact inverse semi-group, this mapping (cf. Regular element) is continuous if and only if
is a topological group. In a locally compact inverse semi-group, this mapping (cf. Regular element) is continuous if and only if 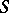 is weakly uniform. In a weakly-uniform semi-group the maximal subgroups are closed. This property need not hold in an arbitrary locally compact semi-group.
is weakly uniform. In a weakly-uniform semi-group the maximal subgroups are closed. This property need not hold in an arbitrary locally compact semi-group.
An arbitrary compact semi-group 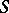 contains a closed kernel
contains a closed kernel 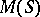 (cf. Kernel of a semi-group), which is a completely-simple semi-group. In particular,
(cf. Kernel of a semi-group), which is a completely-simple semi-group. In particular, 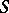 has idempotents. The structure of compact, completely-simple (completely
has idempotents. The structure of compact, completely-simple (completely  -simple) semi-groups is described by a theorem analogous to Rees' theorem on discrete completely-simple (completely
-simple) semi-groups is described by a theorem analogous to Rees' theorem on discrete completely-simple (completely  -simple) semi-groups (cf. Rees semi-group of matrix type). The analogue of Rees' theorem holds for weakly-uniform semi-groups, but not, in general, for locally compact semi-groups [10].
-simple) semi-groups (cf. Rees semi-group of matrix type). The analogue of Rees' theorem holds for weakly-uniform semi-groups, but not, in general, for locally compact semi-groups [10].
A semi-group 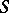 is called a thread if
is called a thread if  can be linearly ordered in such a way that
can be linearly ordered in such a way that  becomes a connected topological semi-group under the order (interval) topology. A semi-group
becomes a connected topological semi-group under the order (interval) topology. A semi-group 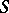 with zero 0 and identity
with zero 0 and identity  is called a standard thread (or
is called a standard thread (or 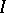 -semi-group) if
-semi-group) if 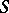 is a thread and if 0 and
is a thread and if 0 and  are the least and largest elements of
are the least and largest elements of 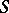 . There is a complete description of standard threads [2]. A compact semi-group with identity
. There is a complete description of standard threads [2]. A compact semi-group with identity  is called irreducible if it is connected and does not contain a proper connected closed sub-semi-group
is called irreducible if it is connected and does not contain a proper connected closed sub-semi-group 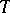 for which
for which 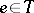 and
and 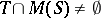 . Connected compact semi-groups with identity contain irreducible semi-groups as closed sub-semi-groups. The irreducible semi-groups can be described as follows: An irreducible semi-group
. Connected compact semi-groups with identity contain irreducible semi-groups as closed sub-semi-groups. The irreducible semi-groups can be described as follows: An irreducible semi-group 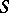 is commutative, the Green equivalence relation
is commutative, the Green equivalence relation 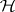 (cf. Green equivalence relations) is a closed congruence on
(cf. Green equivalence relations) is a closed congruence on 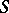 , and
, and 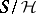 is a standard thread.
is a standard thread.
The "minimal blocks" of a topological semi-group are the closures of its monogenic sub-semi-groups, called monothetic semi-groups. For a compact monothetic semi-group 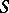 the kernel
the kernel 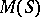 is a compact monothetic group. The compact monothetic semi-groups have been completely described [9]. Weakly-uniform monothetic semi-groups are either compact or discrete. There is an example [13] of a monothetic locally compact semi-group which is neither discrete nor compact.
is a compact monothetic group. The compact monothetic semi-groups have been completely described [9]. Weakly-uniform monothetic semi-groups are either compact or discrete. There is an example [13] of a monothetic locally compact semi-group which is neither discrete nor compact.
A character of a commutative topological semi-group with identity is a non-zero continuous homomorphism into the multiplicative semi-group of complex numbers of modulus 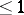 . The set of all characters
. The set of all characters  forms a commutative topological semi-group with identity with respect to pointwise multiplication (cf. Character of a semi-group) and the compact-open topology. One says that the (Pontryagin) duality theorem holds for a commutative topological semi-group with identity if the canonical homomorphism from
forms a commutative topological semi-group with identity with respect to pointwise multiplication (cf. Character of a semi-group) and the compact-open topology. One says that the (Pontryagin) duality theorem holds for a commutative topological semi-group with identity if the canonical homomorphism from 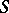 into the semi-group of characters of
into the semi-group of characters of  is a topological isomorphism "onto" . The duality theorem is true for a commutative compact semi-group
is a topological isomorphism "onto" . The duality theorem is true for a commutative compact semi-group 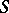 with identity if and only if
with identity if and only if 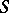 is an inverse semi-group and its sub-semi-group of idempotents forms a totally-disconnected space. Necessary and sufficient conditions have been found [12] for the duality theorem to hold for a commutative locally compact semi-group. One of the necessary conditions is that the semi-group be weakly uniform.
is an inverse semi-group and its sub-semi-group of idempotents forms a totally-disconnected space. Necessary and sufficient conditions have been found [12] for the duality theorem to hold for a commutative locally compact semi-group. One of the necessary conditions is that the semi-group be weakly uniform.
An important subclass of commutative compact semi-groups are the compact semi-lattices (cf. Idempotents, semi-group of). A compact semi-lattice admits a unique topology, up to a homeomorphism. The description of certain types of topological semi-groups leads to metric semi-groups. A metric 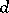 on a topological semi-group
on a topological semi-group  is called invariant if
is called invariant if 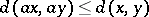 and
and 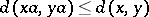 for all
for all 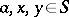 . A topological semi-group is called metric if there exists an invariant metric on
. A topological semi-group is called metric if there exists an invariant metric on 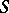 inducing the topology on
inducing the topology on 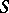 . Every compact semi-group is a projective limit of compact metric semi-groups. Every totally-disconnected compact semi-group is a projective limit of finite semi-groups.
. Every compact semi-group is a projective limit of compact metric semi-groups. Every totally-disconnected compact semi-group is a projective limit of finite semi-groups.
Certain generalizations of topological semi-groups have been considered: semi-groups with a non-Hausdorff space, and semi-topological semi-groups, that is, a topological space on which there is defined an associative binary operation such that all left and right inner translations are continuous mappings.
References
| [1] | A.B. Paalman-de Miranda, "Topological semigroups" , Math. Centre , Amsterdam (1964) |
| [2] | K.H. Hofmann, P.S. Mostert, "Elements of compact semigroups" , C.E. Merrill (1966) |
| [3] | J. Berglund, K. Hofmann, "Compact semitopological semigroups and weakly almost periodic functions" , Springer (1967) |
| [4] | K. Hofmann, M. Mislove, A. Stralka, "The Pontryagin duality of compact 0-dimensional semilattices and its application" , Springer (1974) |
| [5] | K. Hofmann, A. Stralka, "The algebraic theory of compact Lawson semilattices. Applications of Galois connections to compact semilattices" Diss. Math. , 137 (1976) |
| [6] | K. Hofmann, "Topological semigroups: history, theory, applications" Jahresber. Deutsch. Math.-Verein. , 78 (1976) pp. 9–59 |
| [7] | A.D. Wallace, "The structure of topological semigroups" Bull. Amer. Math. Soc. , 61 (1955) pp. 95–112 |
| [8] | J.H. Williamson, "Harmonic analysis on semigroups" J. London Math. Soc. , 42 (1967) pp. 1–41 |
| [9] | E. Hewitt, "Compact monothetic semigroups" Duke Math. J. , 23 (1956) pp. 447–457 |
| [10] | L.B. Shneperman, "The Rees theorem for weakly uniform semigroups" Semigroup Forum , 23 (1981) pp. 261–273 |
| [11] | D. Day, "Expository lectures on topological semigroups" M.A. Arbib (ed.) , Algebraic Theory of Machines, Languages and Semigroups , Acad. Press (1968) pp. 269–296 |
| [12] | L.B. Shneperman, "On the theory of characters of locally bicompact topological semigroups" Math. USSR Sb. , 6 : 4 (1968) pp. 471–492 Mat. Sb. , 77 : 4 (1968) pp. 508–532 |
| [13] | E.G. Zelen'yuk, "On Pontryagin's alternative for topological semigroups" Mat. Zametki , 44 : 3 (1988) pp. 402–403 (In Russian) |
Comments
In the years since 1970, the study of topological semi-groups has followed various main trends: compact semi-topological and right- (respectively, left-) topological semi-groups, compact semi-lattices and continuous lattices (cf. Continuous lattice) and the Lie theory of semi-groups.
A right-topological semi-group is a semi-group in which all translations 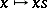 are continuous. (Some authors use the opposite notation.) Compact semi-topological semi-groups and compact right-topological semi-groups, like topological semi-groups, contain idempotents and possess completely simple kernels (minimal two-sided ideals), but, in contrast to compact topological semi-groups, these need no longer be closed. The existence of a kernel in a compact topological semi-group has been used in probability theory on topological groups and semi-groups (cf. [a9], [a10]). Compact semi-topological semi-groups occur as semi-groups of linear operators in the strong operator topology and are crucial in the theory of weakly almost-periodic functions on a topological group or semi-group (cf. [3], [a1], [a2], and Almost-periodic function on a group), and they arise as compactifications of Lie groups (cf. [a9], [a11], and Lie group). Harmonic analysis and representation theory call for semi-topological semi-groups too (cf. [a3], [a4]). Right-topological semi-groups emerge in topological dynamics (cf. [a5], [a9], [a11]), and, since the Stone–Čech compactification
are continuous. (Some authors use the opposite notation.) Compact semi-topological semi-groups and compact right-topological semi-groups, like topological semi-groups, contain idempotents and possess completely simple kernels (minimal two-sided ideals), but, in contrast to compact topological semi-groups, these need no longer be closed. The existence of a kernel in a compact topological semi-group has been used in probability theory on topological groups and semi-groups (cf. [a9], [a10]). Compact semi-topological semi-groups occur as semi-groups of linear operators in the strong operator topology and are crucial in the theory of weakly almost-periodic functions on a topological group or semi-group (cf. [3], [a1], [a2], and Almost-periodic function on a group), and they arise as compactifications of Lie groups (cf. [a9], [a11], and Lie group). Harmonic analysis and representation theory call for semi-topological semi-groups too (cf. [a3], [a4]). Right-topological semi-groups emerge in topological dynamics (cf. [a5], [a9], [a11]), and, since the Stone–Čech compactification  of the additive semi-group of natural numbers is a right-topological semi-group, in number theory (Ramsey theory, cf. Ramsey theorem). The existence of idempotents in
of the additive semi-group of natural numbers is a right-topological semi-group, in number theory (Ramsey theory, cf. Ramsey theorem). The existence of idempotents in 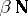 has been used for a new proof of the van der Waerden theorem on arithmetic progressions (cf. [a9]).
has been used for a new proof of the van der Waerden theorem on arithmetic progressions (cf. [a9]).
In [5] it was recognized that the concept of a compact semi-lattice in which every element has a neighbourhood base of sub-semi-lattices agrees with the concept of a continuous lattice. Therefore, the theory of compact semi-lattices is linked with the theory of continuous lattices and its generalizations.
The Lie theory of semi-groups deals with sub-semi-groups of Lie groups and with topological semi-groups which can be imbedded into a Lie group, at least locally about their identity element (cf. [a8], [a9]). If  is a sub-semi-group of a Lie group
is a sub-semi-group of a Lie group 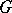 with Lie algebra
with Lie algebra 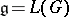 , then the set
, then the set 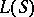 of all
of all 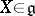 with
with 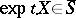 for all
for all 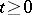 is a convex cone
is a convex cone 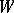 satisfying
satisfying 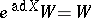 for all
for all 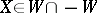 , where
, where 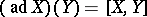 . Such cones are called Lie wedges. If
. Such cones are called Lie wedges. If 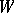 generates
generates 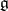 as a Lie algebra, then the semi-group algebraically generated by
as a Lie algebra, then the semi-group algebraically generated by 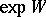 in
in 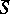 contains inner points with respect to
contains inner points with respect to  . If
. If 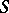 is invariant under all inner automorphisms, then
is invariant under all inner automorphisms, then 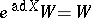 for all
for all 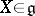 . Such cones are called invariant. Invariant pointed cones
. Such cones are called invariant. Invariant pointed cones 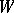 with inner points exist in a Lie algebra
with inner points exist in a Lie algebra 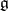 only if
only if 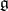 contains a compactly imbedded Cartan subalgebra
contains a compactly imbedded Cartan subalgebra 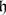 ; in this case they can be classified with the aid of the intersections
; in this case they can be classified with the aid of the intersections 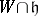 (cf. [a9]). S. Lie's fundamental theorems have analogues in the Lie theory of semi-groups (cf. [a9], [a11]). The Lie theory of semi-groups is applied in such areas as chronogeometry in general relativity (cf. [a7]), non-linear control theory on manifolds and Lie groups (cf. [a9]) and representation theory (cf. [a9]).
(cf. [a9]). S. Lie's fundamental theorems have analogues in the Lie theory of semi-groups (cf. [a9], [a11]). The Lie theory of semi-groups is applied in such areas as chronogeometry in general relativity (cf. [a7]), non-linear control theory on manifolds and Lie groups (cf. [a9]) and representation theory (cf. [a9]).
References
| [a1] | J.F. Berglund, H.D. Junghenn, P. Milnes, "Compact right topological semigroups and generalizations of almost periodicity" , Lect. notes in math. , 663 , Springer (1978) |
| [a2] | J.F. Berglund, H.D. Junghenn, P. Milnes, "Analysis on semigroups" , Wiley (1989) |
| [a3] | C.D. Dunkl, D. Ramirez, "Representations of commutative semitopological semigroups" , Lect. notes in math. , 435 , Springer (1975) |
| [a4] | H.A.M. Dzinotyiweyi, "The analogue of the group algebra for topological semigroups" , Pitman (1984) |
| [a5] | R. Ellis, "Lectures in topological dynamics" , Benjamin (1969) |
| [a6] | G. Gierz, K.H. Hofmann, K. Keimel, J.D. Lawson, M.V. Mislove, D.S. Scott, "A compendium of continuous lattices" , Springer (1980) |
| [a7] | J. Hilgert, K.H. Hofmann, "The causal structure of homogeneous manifolds" Math. Scand. , 67 (1990) pp. 119–144 |
| [a8] | J. Hilgert, K.H. Hofmann, J.D. Lawson, "Lie groups, convex cones, and topological theory of semigroups" , Oxford Univ. Press (1989) |
| [a9] | K.H. Hofmann (ed.) J.D. Lawson (ed.) J.S. Pym (ed.) , The analytical and topological theory of semigroups , de Gruyter (1990) |
| [a10] | A. Mukherjea, N. Tserpes, "Measures on topological semigroups" , Lect. notes in math. , 547 , Springer (1976) |
| [a11] | W.A.F. Ruppert, "Compact semitopological semigroups: an intrinsic theory" , Lect. notes in math. , 1079 , Springer (1984) |
Topological semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_semi-group&oldid=12760