Topological module
left topological module
An Abelian topological group 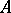 that is a module over a topological ring
that is a module over a topological ring 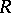 , in which the multiplication mapping
, in which the multiplication mapping  , taking
, taking 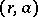 to
to 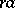 , is required to be continuous. A right topological module is defined analogously. Every submodule
, is required to be continuous. A right topological module is defined analogously. Every submodule  of a topological module
of a topological module 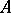 is a topological module. If the module
is a topological module. If the module 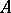 is separated and
is separated and 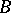 is closed in
is closed in 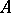 , then
, then 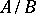 is a separated module. A direct product of topological modules is a topological module. The completion
is a separated module. A direct product of topological modules is a topological module. The completion 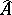 of the module
of the module 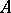 as an Abelian topological group can be given the natural structure of a topological module over the completion
as an Abelian topological group can be given the natural structure of a topological module over the completion 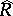 of the ring
of the ring  .
.
A topological 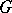 -module, where
-module, where 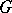 is a topological group, is an Abelian topological group
is a topological group, is an Abelian topological group  that is a
that is a 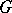 -module, where the multiplication mapping
-module, where the multiplication mapping 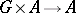 is required to be continuous.
is required to be continuous.
References
| [1] | N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Topological module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_module&oldid=16407