Difference between revisions of "Topological field"
(Importing text file) |
m (some TeX) |
||
| Line 1: | Line 1: | ||
| − | A [[Topological ring|topological ring]] | + | A [[Topological ring|topological ring]] $K$ that is a [[Field|field]], where in addition it is required that the inverse mapping $a\mapsto a^{-1}$ is continuous on $K\setminus \{0\}$. Any subfield $P$ of a topological field $K$, and the closure $\overline{P}$ of $P$ in $K$, is also a topological field. |
The only connected locally compact topological fields are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t0930609.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306010.png" /> (cf. also [[Locally compact skew-field|Locally compact skew-field]]). Every normed field is a topological field with respect to the topology induced by the norm (cf. [[Norm|Norm]]; [[Norm on a field|Norm on a field]]). If there exist two real-valued norms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306012.png" /> on a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306013.png" />, each of which makes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306014.png" /> a complete topological field, and if the topologies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306016.png" /> induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306018.png" /> are distinct, then the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306019.png" /> is algebraically closed. The field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306020.png" /> is the unique real-normed extension of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306021.png" />. | The only connected locally compact topological fields are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t0930609.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306010.png" /> (cf. also [[Locally compact skew-field|Locally compact skew-field]]). Every normed field is a topological field with respect to the topology induced by the norm (cf. [[Norm|Norm]]; [[Norm on a field|Norm on a field]]). If there exist two real-valued norms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306012.png" /> on a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306013.png" />, each of which makes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306014.png" /> a complete topological field, and if the topologies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306016.png" /> induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306018.png" /> are distinct, then the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306019.png" /> is algebraically closed. The field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306020.png" /> is the unique real-normed extension of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093060/t09306021.png" />. | ||
Revision as of 03:52, 24 January 2013
A topological ring $K$ that is a field, where in addition it is required that the inverse mapping $a\mapsto a^{-1}$ is continuous on $K\setminus \{0\}$. Any subfield $P$ of a topological field $K$, and the closure $\overline{P}$ of $P$ in $K$, is also a topological field.
The only connected locally compact topological fields are  and
and  (cf. also Locally compact skew-field). Every normed field is a topological field with respect to the topology induced by the norm (cf. Norm; Norm on a field). If there exist two real-valued norms
(cf. also Locally compact skew-field). Every normed field is a topological field with respect to the topology induced by the norm (cf. Norm; Norm on a field). If there exist two real-valued norms  and
and  on a field
on a field  , each of which makes
, each of which makes  a complete topological field, and if the topologies
a complete topological field, and if the topologies  and
and 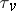 induced by
induced by  and
and  are distinct, then the field
are distinct, then the field  is algebraically closed. The field
is algebraically closed. The field 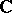 is the unique real-normed extension of the field
is the unique real-normed extension of the field  .
.
On every field of infinite cardinality  there exist precisely
there exist precisely  distinct topologies which make it a topological field. The topology of a topological field is either anti-discrete or completely regular. Topological fields with non-normal topologies, as well as topological fields with a normal but not hereditarily-normal topology, have been constructed. Topological fields are either connected or totally disconnected. There exists a connected topological field of arbitrary finite characteristic. It is unknown (1992) whether every topological field can be imbedded as a subfield in a connected topological field. In contrast to topological rings and linear topological spaces, not every completely-regular topological space can be imbedded as a subspace of a topological field. For example, a pseudo-compact (in particular, compact) subspace of a topological field is always metrizable. However, every completely-regular space admitting a continuous bijection onto a metric space can be imbedded as a subspace in some topological field. If the topological field
distinct topologies which make it a topological field. The topology of a topological field is either anti-discrete or completely regular. Topological fields with non-normal topologies, as well as topological fields with a normal but not hereditarily-normal topology, have been constructed. Topological fields are either connected or totally disconnected. There exists a connected topological field of arbitrary finite characteristic. It is unknown (1992) whether every topological field can be imbedded as a subfield in a connected topological field. In contrast to topological rings and linear topological spaces, not every completely-regular topological space can be imbedded as a subspace of a topological field. For example, a pseudo-compact (in particular, compact) subspace of a topological field is always metrizable. However, every completely-regular space admitting a continuous bijection onto a metric space can be imbedded as a subspace in some topological field. If the topological field  contains at least one countable non-closed subset, then there exists a weakest metrizable topology on
contains at least one countable non-closed subset, then there exists a weakest metrizable topology on 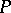 turning it into a topological field.
turning it into a topological field.
For a topological field 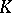 one defines the completion
one defines the completion  — a complete topological ring in which
— a complete topological ring in which  is imbedded as an everywhere-dense subfield. The ring
is imbedded as an everywhere-dense subfield. The ring 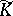 can have zero divisors. However, the completion of every real-normed topological field is a real-normed topological field.
can have zero divisors. However, the completion of every real-normed topological field is a real-normed topological field.
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [2] | W. Wieslaw, "Topological fields" , M. Dekker (1988) |
| [3] | D.B. Shakhmatov, "Cardinal invariants of topological fields" Soviet. Math. Dokl. , 28 : 1 (1983) pp. 209–294 Dokl. Akad. Nauk SSSR , 271 : 6 (1983) pp. 1332–1336 |
Topological field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topological_field&oldid=16292