Tonelli plane variation

A numerical characteristic of a function of two variables, by means of which one defines the class of functions of bounded variation in the sense of Tonelli. Suppose that 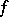is a function given on the rectangle 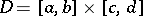. Assume that the functions

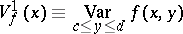and

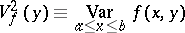are Lebesgue measurable (the first on the interval 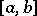, the second on 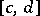). If

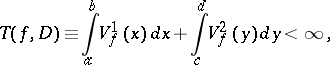then one says that the function 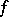has bounded (finite, or: is of bounded (finite)) Tonelli plane variation on the rectangle 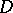, and the class of all such functions is denoted by 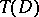. This definition was proposed by L. Tonelli (cf. [1], [2]). For continuous functions, however, another characterization (in terms of the Banach indicatrix) of the class can be found in an earlier paper of S. Banach [4]. If the function 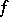is continuous on the rectangle 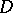, then the surface 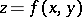has finite area if and only if 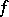belongs to 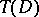(cf. Tonelli theorem).

References

[1]	L. Tonelli, "Sur la quadrature des surfaces" C.R. Acad. Sci. Paris , 182 (1926) pp. 1198–1200
[2]	L. Tonelli, "Sulla quadratura delle superficie" Atti Accad. Naz. Lincei , 3 (1926) pp. 357–363; 445–450; 633–658
[3]	A.G. Vitushkin, "On higher-dimensional variations" , Moscow (1955) (In Russian)
[4]	S. Banach, "Sur les lignes rectifiables et les surfaces dont l'aire est finie" Fund. Math. , 7 (1925) pp. 225–236
[5]	S. Saks, "Theory of the integral" , Hafner (1952) pp. 169 (Translated from French)