Tits system
A collection 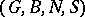 , where
, where 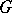 is a group,
is a group,  and
and 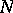 are subgroups and
are subgroups and 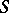 is a subset of
is a subset of 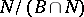 , satisfying the following conditions: 1) the set
, satisfying the following conditions: 1) the set 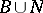 generates the group
generates the group 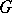 ; 2)
; 2) 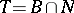 is a normal subgroup of
is a normal subgroup of 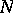 ; 3) the set
; 3) the set 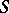 generates the group
generates the group 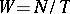 and consists of elements of order 2; 4)
and consists of elements of order 2; 4) 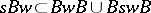 for all
for all  ,
, 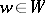 ; and 5)
; and 5) 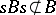 for
for 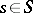 . The group
. The group 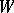 , called the Weyl group of the Tits system
, called the Weyl group of the Tits system 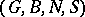 , is a Coxeter group with respect to the system of generators
, is a Coxeter group with respect to the system of generators 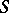 . The correspondence
. The correspondence 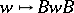 is a bijection from
is a bijection from 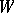 onto the set of double cosets of
onto the set of double cosets of 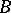 in
in 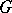 .
.
Examples. a) 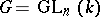 , where
, where 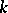 is any field,
is any field, 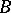 is the subgroup of upper triangular matrices,
is the subgroup of upper triangular matrices, 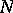 is the subgroup of monomial matrices (so that
is the subgroup of monomial matrices (so that 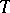 is the subgroup of diagonal matrices and
is the subgroup of diagonal matrices and 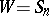 , cf. Monomial matrix), and
, cf. Monomial matrix), and 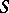 is the set of transpositions
is the set of transpositions 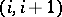 , where
, where 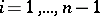 .
.
b) More generally, let 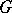 be a connected reductive algebraic group over
be a connected reductive algebraic group over 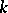 , let
, let 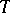 be a maximal torus in
be a maximal torus in 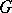 diagonalizable over
diagonalizable over 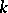 , let
, let 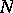 be its normalizer, let
be its normalizer, let 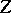 be its centralizer, let
be its centralizer, let 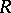 be the root system of
be the root system of 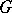 relative to
relative to 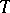 , let
, let 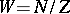 be its Weyl group, and let
be its Weyl group, and let 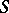 be the set of reflections corresponding to the simple roots. Moreover, let
be the set of reflections corresponding to the simple roots. Moreover, let 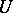 be the unipotent subgroup of
be the unipotent subgroup of 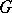 generated by the root subgroups corresponding to the positive roots, and let
generated by the root subgroups corresponding to the positive roots, and let 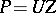 . Then the quadruple
. Then the quadruple 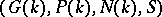 is a Tits system.
is a Tits system.
c) Let 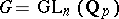 , where
, where 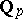 is the field of
is the field of 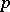 -adic numbers, let
-adic numbers, let 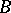 be the subgroup consisting of matrices
be the subgroup consisting of matrices 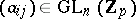 (where
(where 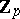 is the ring of
is the ring of 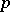 -adic integers), such that
-adic integers), such that 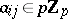 for
for 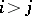 , and let
, and let 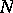 be the subgroup of monomial matrices. Then there exists a subset
be the subgroup of monomial matrices. Then there exists a subset 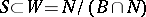 such that the quadruple
such that the quadruple 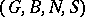 is a Tits system. Here the group
is a Tits system. Here the group 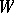 is an infinite Coxeter group of type
is an infinite Coxeter group of type 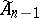 . Analogously one can define Tits systems with Weyl groups of affine type corresponding to other connected reductive groups over local fields.
. Analogously one can define Tits systems with Weyl groups of affine type corresponding to other connected reductive groups over local fields.
Under certain conditions one can assert that a group 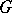 admitting a Tits system is simple. For example, the following conditions are sufficient for this:
admitting a Tits system is simple. For example, the following conditions are sufficient for this:  )
) 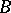 is a solvable group, and is not contained in any proper normal subgroup of
is a solvable group, and is not contained in any proper normal subgroup of 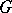 ;
; 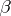 )
) 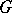 is equal to its own commutator subgroup;
is equal to its own commutator subgroup; 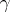 ) the Coxeter group
) the Coxeter group 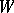 is indecomposable; or
is indecomposable; or 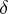 ) the group
) the group 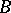 does not contain any non-trivial normal subgroup of
does not contain any non-trivial normal subgroup of 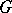 . In this way one can prove the simplicity of the Chevalley groups, in particular of the finite ones (cf. Chevalley group).
. In this way one can prove the simplicity of the Chevalley groups, in particular of the finite ones (cf. Chevalley group).
References
| [1] | J. Tits, "Buildings of spherical type and finite BN-pairs" , Lect. notes in math. , 386 , Springer (1974) |
| [2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) pp. Chapt. 4 (Translated from French) |
Comments
A Tits system is also called a group with a 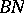 -pair.
-pair.
Let 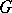 be a
be a  -transitive permutation group on the set
-transitive permutation group on the set 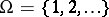 ; then
; then 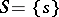 and
and 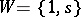 , where
, where  is a permutation in
is a permutation in 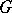 interchanging
interchanging 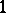 and
and  ,
,  and
and 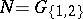 . This gives a Tits system of type
. This gives a Tits system of type 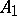 .
.
References
| [a1] | M.A. Ronan, "Lectures on buildings" , Acad. Press (1989) |
Tits system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tits_system&oldid=11480