Tilting theory

Artin algebras.

A finitely-generated module 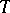over an Artin algebra 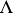(cf. also Artinian module) is called a tilting module if 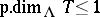and and 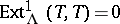there is a short exact sequence 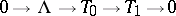with 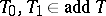. Here, 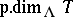denotes the projective dimension of and 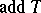is the category of finite direct sums of direct summands of 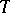(see Tilting module). Dually, a 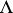-module 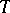is called a cotilting module if the 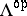-module 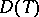is a tilting module, where 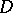denotes the usual duality. If 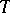is a tilting module and 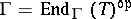, then 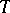is a tilting module over 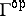. Hence 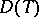is a cotilting 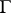-module.

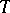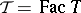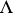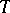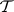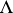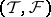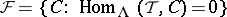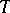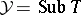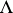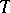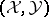Let be a tilting module, and let be the category of finitely-generated -modules generated by . The category is a torsion class in the category of finitely-generated -modules. This yields an associated torsion pair , where . Dually, there is associated with a cotilting module the subcategory of -modules cogenerated by . The category is a torsion-free class and there is an associated torsion pair where .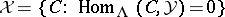

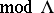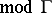An important feature of tilting theory is the following connection between and when 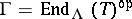for a tilting module 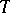: If 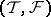denotes the torsion pair in 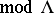associated with 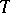and 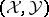the torsion pair associated with 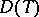, then there are equivalences of categories:

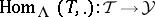and

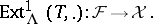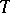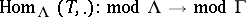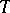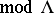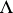(Cf. also Tilting functor.) In the special case where is a projective generator one recovers the Morita equivalence , where is a projective generator of . For a general module , the Artin algebras and 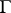may be quite different, but they share many homological properties; in particular, one uses the tilting functors 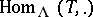and 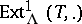in order to transfer properties between 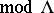and 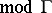. The transfer of information is especially useful when one already knows a lot about and when the torsion pair 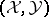splits, that is, when each indecomposable 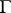-module is in or in 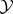. This is the case when 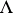is hereditary. In this case, is called a tilted algebra (cf. also Tilted algebra). Tilted algebras have played an important part in representation theory, since many questions can be reduced to this class of algebras.

Tilting theory goes back to the reflection functors introduced by I.N. Bernshtein, I.M. Gel'fand and V.A. Ponomarev [a6] in the early 1970s. A module-theoretic interpretation of these functors was given by M. Auslander, M.I. Platzeck and I. Reiten [a1]. Further generalizations where given by S. Brenner and M.C.R. Butler [a5], where the equivalence 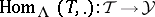was established. The above definitions where given by D. Happel and C.M. Ringel [a12], who developed an extensive theory of tilted algebras. A good reference for the early work in tilting theory is [a4].

An important theoretical development of tilting theory was the connection with derived categories established by Happel [a10]. The functor 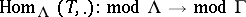when 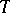is a tilting module induces an equivalence 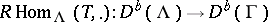, where 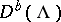denotes the derived category whose objects are the bounded complexes of 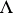-modules.

The set of all tilting modules (up to isomorphism) over a 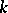-algebra 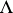, 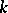an algebraically closed field, has an interesting combinatorial structure: It is a countable simplicial complex . This complex has been investigated by L. Unger in [a21] and [a22], where it was proved that 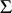is a shellable simplicial complex provided it is finite, and that certain representation-theoretical invariants are reflected by its structure.

Analogues and generalizations.

There is an analogous concept of a tilting sheaf 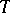for the category 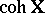of coherent sheaves of a weighted projective line (cf. also Coherent sheaf) as studied in [a9]. The canonical algebras introduced in [a19] can be realized as endomorphism algebras of certain tilting sheaves.

To obtain a common treatment of both the class of tilted algebras and the canonical algebras, in [a13] tilting theory was generalized to hereditary categories 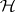, that is, is a connected Abelian 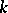-category with vanishing Yoneda functor 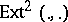and finite-dimensional homomorphism and extension spaces. Here, denotes an algebraically closed field. An object 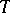in with 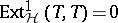such that 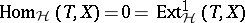implies 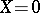, is called a tilting object in 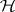. The endomorphism algebra 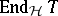of a tilting object 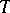is called a quasi-tilted algebra. Tilted algebras and canonical algebras furnish examples for quasi-tilted algebras.

There are two types of hereditary categories with tilting objects: those derived equivalent to 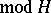for some finite-dimensional hereditary -algebra 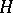and those derived equivalent to some category 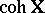of coherent sheaves on a weighted projective line . Two categories are called derived equivalent if their derived categories are equivalent as triangulated categories. In 2000, Happel [a11] proved that these are the only possible hereditary categories with tilting object. This proved a conjecture stated, for example, in [a17].

Generalizations and applications of tilting modules.

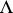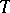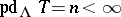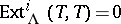A -module is called a generalized tilting module if and for 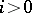and there is an exact sequence 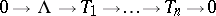with 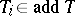. Generalized tilting modules were introduced in [a16]. This concept was generalized to the notion of tilting complexes by J. Rickard [a18], who established some "Morita theory for derived categories" . Let 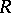be a ring and let 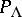be the category of finitely-generated projective 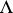-modules. Denote by 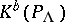the category of bounded complexes over 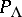modulo homotopy. A complex 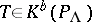is called a tilting complex if 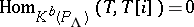for all 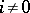(here, denotes the shift functor) and if 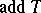generates 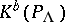as a triangulated category. Rickard proved that two rings 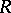and 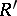are derived equivalent (i.e. their module categories are derived equivalent) if and only if 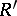is the endomorphism ring of a tilting complex .

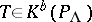The results mentioned above uses tilting modules/objects mainly to compare 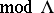and 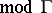, where 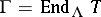for some tilting module/object. There are other approaches, which use tilting modules to describe subcategories of 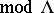. Kerner [a15] and W. Crawley-Boevey and Kerner [a7] used tilting modules to investigate subcategories of regular modules over wild hereditary algebras.

Quasi-hereditary algebras.

Auslander and Reiten [a2] proved that there is a one-to-one correspondence between basic generalized tilting modules and certain covariantly finite subcategories of 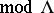. This correspondence was further investigated [a14]. The Auslander–Reiten correspondence was applied to quasi-hereditary algebras by Ringel [a20] and his results served as a basis for applications to Schur algebras by S. Donkin [a8] and to quantum groups by H.H. Andersen [a3]. In dealing with quasi-hereditary algebras and highest-weight categories, the notion of a tilting module is now (2000) used in a related but deviating way, namely for all the objects or modules that have both a 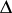-filtration and a -filtration. The isomorphism classes of the indecomposables that have both a -filtration and a -filtration correspond bijectively to the elements of the weight poset, and their direct sum is a tilting module in the sense considered above.

References

[a1]	M. Auslander, M.I. Platzeck, I. Reiten, "Coxeter functors without diagrams" Trans. Amer. Math. Soc. , 250 (1979) pp. 1–12
[a2]	M. Auslander, I. Reiten, "Applications of contravariantly finite subcategories" Adv. Math. , 86 : 1 (1991) pp. 111–152
[a3]	H.H. Andersen, "Tensor products of quantized tilting modules" Commun. Math. Phys. , 149 : 1 (1992) pp. 149–159
[a4]	I. Assem, "Tilting theory - an introduction" , Topics in Algebra , Banach Center Publ. , 26 , PWN (1990) pp. 127–180
[a5]	S. Brenner, M.C.R. Butler, "Generalization of Bernstein–Gelfand–Ponomarev reflection functors" , Proc. Ottawa Conf. on Representation Theory, 1979 , Lecture Notes in Mathematics , 832 , Springer (1980) pp. 103–169
[a6]	I.N. Bernstein, I.M. Gelfand, V.A. Ponomarev, "Coxeter functors and Gabriel's theorem" Russian Math. Surveys , 28 (1973) pp. 17–32 Uspekhi Mat. Nauk. , 28 (1973) pp. 19–33
[a7]	W. Crawley-Boevey, O. Kerner, "A functor between categories of regular modules for wild hereditary algebras" Math. Ann. , 298 (1994) pp. 481–487
[a8]	S. Donkin, "On tilting modules for algebraic groups" Math. Z. , 212 : 1 (1993) pp. 39–60
[a9]	W. Geigle, H. Lenzing, "Perpendicular categories with applications to representations and sheaves" J. Algebra , 144 (1991) pp. 273–343
[a10]	D. Happel, "Triangulated categories in the representation theory of finite dimensional algebras" London Math. Soc. Lecture Notes , 119 (1988)
[a11]	D. Happel, "A characterization of hereditary categories with tilting object" preprint (2000)
[a12]	D. Happel, C.M. Ringel, "Tilted algebras" Trans. Amer. Math. Soc. , 274 (1982) pp. 399–443
[a13]	D. Happel, R. Reiten, S.O. Smalø, "Tilting in abelian categories and quasitilted algebras" Memoirs Amer. Math. Soc. , 575 (1996)
[a14]	D. Happel, L. Unger, "Modules of finite projective dimension and cocovers" Math. Ann. , 306 (1996) pp. 445–457
[a15]	O. Kerner, "Tilting wild algebras" J. London Math. Soc. , 39 : 2 (1989) pp. 29–47
[a16]	Y. Miyashita, "Tilting modules of finite projective dimension" Math. Z. , 193 (1986) pp. 113–146
[a17]	I. Reiten, "Tilting theory and quasitilted algebras" , Proc. Internat. Congress Math. Berlin , II (1998) pp. 109–120
[a18]	J. Rickard, "Morita theory for derived categories" J. London Math. Soc. , 39 : 2 (1989) pp. 436–456
[a19]	C.M. Ringel, "The canonical algebras" , Topics in Algebra , Banach Center Publ. , 26:1 , PWN (1990) pp. 407–432
[a20]	C.M. Ringel, "The category of modules with good filtration over a quasi-hereditary algebra has alost split sequences" Math. Z. , 208 (1991) pp. 209–224
[a21]	L. Unger, "The simplicial complex of tilting modules over quiver algebras" Proc. London Math. Soc. , 73 : 3 (1996) pp. 27–46
[a22]	L. Unger, "Shellability of simplicial complexes arising in representation theory" Adv. Math. , 144 (1999) pp. 221–246