Thue method
A method in the theory of Diophantine approximations, created by A. Thue [1] in connection with the problem of approximating algebraic numbers (cf. Algebraic number) by rational numbers: Find a quantity  such that for each algebraic number
such that for each algebraic number 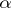 of degree
of degree  the inequality
the inequality
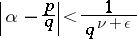 | (1) |
has a finite number of solutions in rational integers 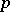 and
and  ,
, 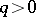 , for any
, for any  , and an infinite number of solutions for any
, and an infinite number of solutions for any  .
.
Thue proved that  . Thue's method is based on properties of a special polynomial
. Thue's method is based on properties of a special polynomial 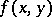 of two variables
of two variables 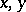 with integer coefficients, and the hypothesis that there exist two solutions of (1) for
with integer coefficients, and the hypothesis that there exist two solutions of (1) for 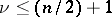 with sufficiently large values of
with sufficiently large values of 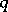 . Thue's theorem has many important applications in number theory. In particular, it implies that the Diophantine equation
. Thue's theorem has many important applications in number theory. In particular, it implies that the Diophantine equation
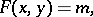 | (2) |
where 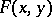 is an irreducible form in the variables
is an irreducible form in the variables  and
and 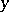 with integer coefficients and of degree
with integer coefficients and of degree 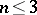 , while
, while  is an integer, cannot have more than a finite number of solutions in integers
is an integer, cannot have more than a finite number of solutions in integers  and
and  .
.
The best possible estimate of the size of  in (1) was obtained by K.F. Roth [2], by generalizing Thue's method to the case of a polynomial in any number of variables, similar to the polynomial
in (1) was obtained by K.F. Roth [2], by generalizing Thue's method to the case of a polynomial in any number of variables, similar to the polynomial 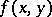 , and making use of the large number of solutions of (1). The result, called the Thue–Siegel–Roth theorem, states that
, and making use of the large number of solutions of (1). The result, called the Thue–Siegel–Roth theorem, states that  for any
for any 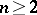 . Thue's method has a generalization to the case of approximation of algebraic numbers by algebraic numbers. Thue's method is a general method for proving the finiteness of the number of integer points on a wide class of curves on algebraic varieties (see Diophantine geometry; Diophantine set). Apart from this, Thue's method has essential deficiencies: it is a non-effective method in the sense that it does not provide an answer to the question whether there exist in fact solutions of the inequalities (1) or the corresponding equations (2) that can be made use of in the proofs. Thus, Thue's method, in solving the question on the finiteness of the number of solutions of equation (2), does not provide the possibility of determining whether an actual equation of this type is solvable and what the sizes of the estimates of the solutions
. Thue's method has a generalization to the case of approximation of algebraic numbers by algebraic numbers. Thue's method is a general method for proving the finiteness of the number of integer points on a wide class of curves on algebraic varieties (see Diophantine geometry; Diophantine set). Apart from this, Thue's method has essential deficiencies: it is a non-effective method in the sense that it does not provide an answer to the question whether there exist in fact solutions of the inequalities (1) or the corresponding equations (2) that can be made use of in the proofs. Thus, Thue's method, in solving the question on the finiteness of the number of solutions of equation (2), does not provide the possibility of determining whether an actual equation of this type is solvable and what the sizes of the estimates of the solutions  are in their dependence on
are in their dependence on 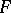 .
.
See also Diophantine approximation, problems of effective.
References
| [1] | A. Thue, "Ueber Annäherungswerte algebraischer Zahlen" J. Reine Angew. Math. , 135 (1909) pp. 284–305 |
| [2] | K.F. Roth, "Rational approximation to algebraic numbers" Mathematika , 2 : 1 (1955) pp. 1–20 |
| [3] | , Problems in the theory of Diophantine approximations , Moscow (1974) (In Russian; translated from English) |
Comments
Thue's method has been extended by C.L. Siegel to obtain  . For a good exposition, see [a1]. This method, known as the Thue–Siegel method, has recently met with spectacular success when P. Vojta [a2] showed how it could be used to give a new proof of the Mordell conjecture. A considerable and very accessible simplification of this proof has been given by E. Bombieri. For other generalizations see Thue–Siegel–Roth theorem.
. For a good exposition, see [a1]. This method, known as the Thue–Siegel method, has recently met with spectacular success when P. Vojta [a2] showed how it could be used to give a new proof of the Mordell conjecture. A considerable and very accessible simplification of this proof has been given by E. Bombieri. For other generalizations see Thue–Siegel–Roth theorem.
References
| [a1] | E. Landau, "Vorlesungen über Zahlentheorie" , Chelsea, reprint (1969) |
| [a2] | P. Vojta, "Siegel's theorem in the compact case" Ann. of Math. (Forthcoming) |
Thue method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thue_method&oldid=13235