Difference between revisions of "Thompson-McKay series"
m (links) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 175 formulas, 160 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | According to the classification theorem, the simple finite groups (cf. also [[Simple finite group|Simple finite group]]) consist of the cyclic groups of prime order (cf. also [[Cyclic group|Cyclic group]]), the alternating groups of degree at least $5$ (cf. also [[Alternating group|Alternating group]]), the Chevalley and twisted Chevalley groups (cf. also [[Chevalley group|Chevalley group]]), the Tits group and the $26$ sporadic simple groups (cf. also [[Sporadic simple group|Sporadic simple group]]). The first five sporadic groups were described by E. Mathieu in the 19th century [[#References|[a24]]], [[#References|[a25]]]. No further sporadic groups were found until Z. Janko's discovery of the first modern sporadic group in 1964 [[#References|[a14]]], [[#References|[a15]]]. Evidence for the existence of the largest of the sporadic groups, $\mathcal{M}$, was found independently by B. Fischer and R.L. Griess in 1973. This group is now known as the monster and has order | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t1200704.png"/></td> </tr></table> |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t1200705.png"/></td> </tr></table> |
| − | Even before Griess's construction [[#References|[a12]]] of | + | \begin{equation*} = 2 ^ { 46 } . 3 ^ { 20 } . 5 ^ { 9 } . 7 ^ { 6 } . 11 ^ { 2 } . 13 ^ { 3 }. \end{equation*} |
| + | |||
| + | \begin{equation*} .17.19 .23 .29 .31 .41 .47 .59 .71. \end{equation*} | ||
| + | |||
| + | Even before Griess's construction [[#References|[a12]]] of $\mathcal{M}$ in 1981, intriguing connections between $\mathcal{M}$ and other areas of mathematics had been noted: | ||
Define | Define | ||
| − | + | \begin{equation*} \Gamma _ { 0 } ( N ) = \left\{ \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} ( 2 , \mathbf{Z} ) : c \equiv 0 ( \operatorname { mod } N ) \right\}, \end{equation*} | |
| − | and for each prime number | + | and for each prime number $p$, let $\Gamma _ { 0 } ( p ) + = \langle \Gamma _ { 0 } ( p ) , \left( \begin{array} { c c } { 0 } & { - 1 } \\ { p } & { 0 } \end{array} \right) \rangle$. Any discrete subgroup $G$ of $\operatorname{SL} ( 2 , \mathbf R )$ acts on the upper half of the complex plane by fractional-linear transformations (cf. also [[Fractional-linear mapping|Fractional-linear mapping]]). The corresponding quotient space has the structure of a [[Riemann surface|Riemann surface]]. If this surface is isomorphic to a sphere (with a finite number of points removed, corresponding to the orbits of the fixed points of the parabolic elements of $G$), then $G$ is said to have genus zero. In 1974, A.P. Ogg [[#References|[a27]]] observed that the primes dividing the order of $\mathcal{M}$ are also the primes for which the group $\Gamma _ { 0 } ( p ) +$ has genus zero. |
| − | Suppose | + | Suppose $G$ has genus zero; then a generator for the function field of $G$ is called a Hauptmodul. Suppose further that $G$ is commensurable with $\operatorname{SL} ( 2 , {\bf Z} )$ and that $G$ contains $z \mapsto z + k$ if and only if $k \in \mathbf{Z}$; then $G$ has a Hauptmodul of the form: |
| − | + | \begin{equation*} \frac { 1 } { q } + a _ { 0 } + a _ { 1 } q + a _ { 2 } q ^ { 2 } + \ldots , \quad q = \operatorname { exp } ( 2 \pi i z ). \end{equation*} | |
| − | This form is unique except for the choice of | + | This form is unique except for the choice of $a_{0}$. For example $\operatorname{SL} ( 2 , {\bf Z} )$ has a Hauptmodul |
| − | + | \begin{equation*} J ( z ) = j ( z ) - 744 = \sum _ { k } c _ { k } q ^ { k } = \end{equation*} | |
| − | + | \begin{equation*} = \frac { 1 } { q } + 196884 q + 21493760 q ^ { 2 } + 864299970 q ^ { 3 } + \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007032.png"/></td> </tr></table> |
| − | In 1978, J. McKay observed in a letter to J.G. Thompson that the coefficient | + | In 1978, J. McKay observed in a letter to J.G. Thompson that the coefficient $c_1$ is $196883 + 1$ and that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007035.png"/> is the degree of the smallest non-trivial irreducible complex representation of $\mathcal{M}$. Thompson [[#References|[a31]]] extended this observation by noting that the coefficients $a_1$, $a _2$, $a_3$, $a_4$, and $a_5$ of $J$ are simple linear combinations of the seven smallest irreducible degrees of $\mathcal{M}$. He also asked whether there exists a graded $\mathcal{M}$-module $V ^ { \natural } = \oplus _ { n } V _ { n }$, now known as the moonshine module, such that |
| − | + | \begin{equation*} J ( z ) = \sum _ { n } \operatorname { Tr } ( e | _{V _ { n }} ) q ^ { n } \end{equation*} | |
| − | where | + | where $e$ is the identity element of $\mathcal{M}$. |
| − | In 1979, J.H. Conway and S.P. Norton [[#References|[a7]]] coined the term "moonshine" for the study of the links between modular functions and the sporadic simple groups (cf. also [[Modular group]]; [[Modular form]]; [[Modular function]]). They generalized the observations of McKay and Thompson by attaching to each element | + | In 1979, J.H. Conway and S.P. Norton [[#References|[a7]]] coined the term "moonshine" for the study of the links between modular functions and the sporadic simple groups (cf. also [[Modular group]]; [[Modular form]]; [[Modular function]]). They generalized the observations of McKay and Thompson by attaching to each element $g \in \mathcal{M}$ a genus-zero group $G _ { g }$, depending only on the [[conjugacy class]] of $g$, with Hauptmodul: |
| − | + | \begin{equation*} j_g ( z ) = \frac { 1 } { q } + a _ { 1 } ( g ) q + a _ { 2 } ( g ) q ^ { 2 } + \dots \end{equation*} | |
| − | with | + | with $j _ { e } ( z ) = J ( z )$. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007054.png"/>, $g \in \mathcal{M}$, are now known as the Thompson–McKay series. Conway and Norton conjectured that $\operatorname { Tr } ( g |_{ V _ n} ) = a _ { n } ( g )$, so that for each $n \geq - 1$ the mapping $g \mapsto a _ { n } ( g )$ defines a character $\mathcal{M}$ (cf. also [[Character of a group|Character of a group]]), which they called the $n$th Head character. They also conjectured identities between the Thompson–McKay series, which they called the replication identities: |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007061.png"/></td> </tr></table> |
| − | where | + | where $Q _ { m , j_g }$ is the unique polynomial in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007063.png"/> such that |
| − | + | \begin{equation*} Q_{ m ,\, j_{ g} } - \frac { 1 } { q ^ { m } } \in q \mathbf{Z} [ [ q ] ]. \end{equation*} | |
These conjectures, and others contained in [[#References|[a7]]], constitute the moonshine conjectures. | These conjectures, and others contained in [[#References|[a7]]], constitute the moonshine conjectures. | ||
| − | Given the character table of | + | Given the character table of $\mathcal{M}$ (which was computed by B. Fischer, D. Livingstone and M.P. Thorne) and the Hauptmoduls <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007066.png"/>, $g \in \mathcal{M}$, Thompson observed that the mapping $g \mapsto a _ { n } ( g )$ is a virtual character of $\mathcal{M}$ for all $n$ if certain congruence conditions hold for a finite number of the $a_n ( g )$. He also showed that if $g \mapsto a _ { n } ( g )$ is a proper character for $\leq 1200$, then it is a proper character for all $n \geq 1$. Thus, in principle, the proof of the existence of $V ^ { \natural }$ can be reduced to a finite computation. Using these methods, A.O.L. Atkin, P. Fong and S.D. Smith [[#References|[a10]]], [[#References|[a30]]] showed that the Head characters are indeed virtual characters of $\mathcal{M}$ and gave very strong evidence that they are proper characters. |
| − | These calculations, however, did not give any information leading to a more conceptual understanding of | + | These calculations, however, did not give any information leading to a more conceptual understanding of $V ^ { \natural }$ and the moonshine conjectures. Another approach to $V ^ { \natural }$ was suggested by the explanations by J. Lepowsky [[#References|[a20]]] and V.G. Kac [[#References|[a16]]] of another observation of McKay that the coefficients of $j ^ { 1 / 3 }$ appear to be character degrees of the complex [[Lie group|Lie group]] $E _ { 8 }$. The underlying structure in this case is that of the affine Kac–Moody Lie algebra $\hat { E } _ { 8 }$ (cf. also [[Kac–Moody algebra|Kac–Moody algebra]]). The corresponding construction for $V ^ { \natural }$ was found by I. Frenkel, Lepowsky and A. Meurman [[#References|[a11]]]. The additional structure is that of a [[vertex operator algebra]]. R.E. Borcherds [[#References|[a2]]], [[#References|[a5]]], [[#References|[a17]]] defined a (real) [[vertex algebra]] to be a [[Vector space|vector space]] $V$ with an infinite number of bilinear products $V \times V \rightarrow \mathbf{R}$, $( u , v ) \mapsto u _ { n } v$ for $u , v \in V$, $n \in \mathbf{Z}$, such that: |
| − | V.1) | + | V.1) $u _ { n } v = 0$ for all $n$ sufficiently large (depending on $u$ and $v$); |
V.2) (the "Jacobi identity" ) | V.2) (the "Jacobi identity" ) | ||
| − | + | \begin{equation*} \sum _ { i \geq 0 } \left( \begin{array} { c } { m } \\ { i } \end{array} \right) ( u _ { q + i } v ) _ { m + n - i } w = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t12007093.png"/></td> </tr></table> |
| − | for all | + | for all $u , v , w \in V$ and for all integers $m$, $n$ and $q$; |
| − | V.3) there is an element | + | V.3) there is an element $1 \in V$ such that, for all $v \in V$, $v _ { n } 1 = 0$ if $n \geq 0$ and $v _{- 1}1 = v$. Also, $1 _ { - 1 } = \operatorname { id}$ (the identity transformation on $V$) and $1 _ { n } = 0$ for $n \neq - 1$. |
| − | A vertex operator algebra (VOA) is a vertex algebra which incorporates the action of the Virasoro Lie algebra (cf. also [[Virasoro algebra|Virasoro algebra]]). Frenkel, Lepowsky and Meurman constructed | + | A vertex operator algebra (VOA) is a vertex algebra which incorporates the action of the Virasoro Lie algebra (cf. also [[Virasoro algebra|Virasoro algebra]]). Frenkel, Lepowsky and Meurman constructed $V ^ { \natural }$ as a vertex operator algebra of conformal dimension $24$. They made a crucial link between the vertex operator algebra structure of $V ^ { \natural }$ and Griess's construction of $\mathcal{M}$ via the Griess algebra and were thus able to show that $V ^ { \natural }$ is an $\mathcal{M}$-module. Their construction provides explicit formulas for the graded traces of elements of $\mathcal{M}$ which commute with an element in the class 2B (Atlas notation, cf. [[#References|[a1]]]) in $\mathcal{M}$. For example, the corresponding formula for the $J$ function is: |
| − | + | \begin{equation*} J ( z ) = \end{equation*} | |
| − | + | \begin{equation*} = \frac { 1 } { 2 } \left( \frac { \Theta _ { \Delta } ( q ) } { \eta ( q ) ^ { 24 } } + \frac { \eta ( q ) ^ { 24 } } { \eta ( q ^ { 2 } ) ^ { 24 } } \right) + \end{equation*} | |
| − | + | \begin{equation*} + \frac { 1 } { 2 } \left( 2 ^ { 12 } \frac { \eta ^ { 24 } ( q ) } { \eta ( q ^ { 1 / 2 } ) ^ { 24 } } - 2 ^ { 12 } \frac { \eta ( q ^ { 2 } ) ^ { 24 } \eta ( q ^ { 1 / 2 } ) ^ { 24 } } { \eta ( q ) ^ { 48 } } \right), \end{equation*} | |
| − | where | + | where $\Theta _ { \Lambda } ( q )$ is the theta-function of the [[Leech lattice|Leech lattice]] $\Lambda$ and $\eta ( q ) = q ^ { 1 / 24 } \prod _ { i = 1 } ^ { \infty } ( 1 - q ^ { i } )$. In principle, this gives a case-by-case verification of the moonshine conjectures for these elements. |
| − | To complete the proof of the moonshine conjectures, Borcherds [[#References|[a4]]] exploited the structure of | + | To complete the proof of the moonshine conjectures, Borcherds [[#References|[a4]]] exploited the structure of $V ^ { \natural }$ to construct a Lie algebra, which he called the Monster Lie algebra. The construction also shows that the Monster Lie algebra is a generalized Kac–Moody Lie algebra (GKM Lie algebra), which is defined by Borcherds [[#References|[a3]]] to be a [[Lie algebra|Lie algebra]] $L$ such that: |
| − | 1) | + | 1) $L$ has a $\bf Z$-grading $L = \oplus _ { n \in \mathbf{Z} } L _ { n }$ and $L_i$ is finite dimensional if $i \neq 0$; |
| − | 2) | + | 2) $L$ has an involution $\omega$ such that $\omega : L _ { i } \rightarrow L _ { - i }$ and acts as $- 1$ on $L_0$; |
| − | 3) | + | 3) $L$ has an invariant bilinear form $( \, . \, , \, . \, )$ such that: |
| − | a) | + | a) $( \, . \, , \, . \, )$ is invariant under $\omega$; |
| − | b) | + | b) $L_{ -i}$ and $L_{j}$ are orthogonal if $i \neq j$; |
| − | c) | + | c) $- ( x , \omega ( x ) ) > 0$ if $x$ is a non-zero homogeneous element of $L$ of non-zero degree. |
| − | Remarkably, generalized Kac–Moody Lie algebras have many of the properties of Kac–Moody Lie algebras. In particular, they have "Weyl denominator" formulas, which in the case of the Monster Lie algebra is the product formula for the | + | Remarkably, generalized Kac–Moody Lie algebras have many of the properties of Kac–Moody Lie algebras. In particular, they have "Weyl denominator" formulas, which in the case of the Monster Lie algebra is the product formula for the $j$-function: |
| − | + | \begin{equation*} p ^ { - 1 } \prod _ { \substack{m > 0 \\ n \in \mathbf{Z} } } ( 1 - p ^ { m } q ^ { n } ) ^ { c_{m n} } = j ( w ) - j ( z ) , p = \operatorname { exp } ( 2 \pi i w ) , \quad q = \operatorname { exp } ( 2 \pi i z ). \end{equation*} | |
| − | The monster Lie algebra inherits an action of | + | The monster Lie algebra inherits an action of $\mathcal{M}$ from $V ^ { \natural }$, and so there are also "twisted" versions of the denominator formula, which can be interpreted as the denominator formulas of certain Lie superalgebras related to the Monster Lie algebra [[#References|[a3]]]. Moreover, by the "no-ghost" theorem, which was first discovered in string theory [[#References|[a3]]], [[#References|[a13]]], these twisted versions of the denominator formula provide relations between the Thompson–McKay series of the moonshine module. These relations are exactly the replication identities conjectured by Conway and Norton. |
| − | One consequence of these identities is that each Thompson–McKay series satisfies certain recurrence relations. For the | + | One consequence of these identities is that each Thompson–McKay series satisfies certain recurrence relations. For the $j$-function these recurrences were first found by D.H. Lehmer [[#References|[a19]]] and were rediscovered by K. Mahler [[#References|[a21]]]. These relations determine ${ j}_g = 1 / q + a _ { 1 } ( g ) q +\dots$ if $a _ { 1 } ( g )$, $a _ { 2 } ( g )$, $a _ { 3 } ( g )$, $a_5 ( g )$ and $j _ { g } 2$ are known. In particular, if $g$ has odd order, then the coefficients of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120070/t120070157.png"/> can be calculated once $a _ { 1 } ( g )$, $a _ { 2 } ( g )$, $a _ { 3 } ( g )$, $a_5 ( g )$ are known. The moonshine conjectures now follow from a calculation of the first $5$ coefficients of the Thompson–McKay series and the proof by M. Koike [[#References|[a18]]] that the Hauptmoduls in question also satisfy the replication identities. |
The original moonshine conjectures have been generalized in several directions and there has also been much work on the theory and applications of vertex operator algebras and generalized Kac–Moody Lie algebras. A far from complete list is: Norton's replicable functions [[#References|[a26]]] and generalized moonshine conjectures [[#References|[a23]]], [[#References|[a8]]]; moonshine for other groups [[#References|[a22]]], [[#References|[a28]]]; A.J.E. Ryba's modular moonshine conjectures [[#References|[a29]]], [[#References|[a4]]], [[#References|[a6]]] and the development of the general theory of vertex operator algebras [[#References|[a9]]]. | The original moonshine conjectures have been generalized in several directions and there has also been much work on the theory and applications of vertex operator algebras and generalized Kac–Moody Lie algebras. A far from complete list is: Norton's replicable functions [[#References|[a26]]] and generalized moonshine conjectures [[#References|[a23]]], [[#References|[a8]]]; moonshine for other groups [[#References|[a22]]], [[#References|[a28]]]; A.J.E. Ryba's modular moonshine conjectures [[#References|[a29]]], [[#References|[a4]]], [[#References|[a6]]] and the development of the general theory of vertex operator algebras [[#References|[a9]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J.H. Conway, R.T. Curtis, S.P. Norton, R.A. Parker, R.A. Wilson, "Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J.G. Thackray" , Oxford Univ. Press (1985)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R.E. Borcherds, "Vertex algebras, Kac–Moody algebras, and the Monster" ''Proc. Nat. Acad. Sci. USA'' , '''83''' (1986) pp. 3068–3071</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> R.E. Borcherds, "Monstrous Moonshine and monstrous Lie superalgebras" ''Invent. Math.'' , '''109''' (1992) pp. 405–444</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> R.E. Borcherds, "Modular moonshine. III" ''Duke Math. J.'' , '''93''' (1998) pp. 129–154</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R.E. Borcherds, "Generalized Kac–Moody algebras" ''J. Algebra'' , '''115''' (1988) pp. 501–512</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R.E. Borcherds, A.J.E. Ryba, "Modular Moonshine. II" ''Duke Math. J.'' , '''83''' (1996) pp. 435–459</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> J.H. Conway, S.P. Norton, "Monstrous Moonshine" ''Bull. London Math. Soc.'' , '''11''' (1979) pp. 308–339</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> C. Dong, H. Li, G. Mason, "Modular invariance of trace functions in orbifold theory" ''preprint'' (1997)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> C. Dong, G. Mason, "Vertex operator algebras and Moonshine: a survey" , ''Progress in Algebraic Combinatorics (Fukuoka, 1993)'' , ''Adv. Stud. Pure Math.'' , '''24''' , Math. Soc. Japan (1996) pp. 101–136</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> P. Fong, "Characters arising in the Monster-modular connection" , ''The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979'' , ''Proc. Symp. Pure Math.'' , '''37''' , Amer. Math. Soc. (1980) pp. 557–559</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operators and the monster" , Acad. Press (1988)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> R.L. Griess, "The friendly giant" ''Invent. Math.'' , '''69''' (1982) pp. 1–102</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> P. Goddard, C.B. Thorne, "Compatibility of the dual Pomeron with unitarity and the absence of ghosts in the dual resonance model" ''Phys. Lett. B'' , '''40''' (1972) pp. 235–238</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> Z. Janko, "A new finite simple group with abelian $2$-Sylow subgroups" ''Proc. Nat. Acad. Sci. USA'' , '''53''' (1965) pp. 657–658</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> Z. Janko, "A new finite simple group with abelian Sylow $2$-subgroups and its characterization" ''J. Algebra'' , '''3''' (1966) pp. 147–186</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> V.G. Kac, "An elucidation of: Infinite-dimensional algebras, Dedekind's $ \eta $-function, classical Möbius function and the very strange formula $E _ { 8 } ^ { ( 1 ) }$ and the cube root of the modular invariant $j$" ''Adv. Math.'' , '''35''' : 3 (1980) pp. 264–273</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> V.G. Kac, "Vertex algebras for beginners" , ''Univ. Lecture Ser.'' , '''10''' , Amer. Math. Soc. (1997)</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> M. Koike, "On replication formula and Hecke operators" ''Preprint Nagoya Univ.'' (unpublished)</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> D.H. Lehmer, "Properties of the coefficients of the modular invariant $J ( \tau )$" ''Amer. J. Math.'' , '''64''' (1942) pp. 488–502</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> J. Lepowsky, "Euclidean Lie algebras and the modular function $j$" , ''The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979)'' , ''Proc. Symp. Pure Math.'' , '''37''' , Amer. Math. Soc. (1980) pp. 567–570</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> K. Mahler, "On a class of non-linear functional equations connected with modular functions" ''J. Austral. Math. Soc.'' , '''22A''' (1976) pp. 65–118</td></tr><tr><td valign="top">[a22]</td> <td valign="top"> G. Mason, "$M _ { 24 }$ and certain automorphic forms" , ''Finite groups: coming of age (Montreal, Que., 1982)'' , ''Contemp. Math.'' , '''45''' , Amer. Math. Soc. (1985) pp. 223–244</td></tr><tr><td valign="top">[a23]</td> <td valign="top"> G. Mason, "Finite groups and modular functions" , ''The Arcata Conference on Representations of Finite Groups (Arcata, Calif. 1986)'' , ''Proc. Symp. Pure Math.'' , '''47:1''' , Amer. Math. Soc. (1987) pp. 181–210 (Appendix by S.P. Norton)</td></tr><tr><td valign="top">[a24]</td> <td valign="top"> E. Mathieu, "Memoire sur l'étude des fonctions de plusieurs quantités" ''J. Math. Pures Appl.'' , '''6''' (1861) pp. 241–323</td></tr><tr><td valign="top">[a25]</td> <td valign="top"> E. Mathieu, "Sur les fonctions cinq fois transitives de $24$ quantités" ''J. Math. Pures Appl.'' , '''18''' (1873) pp. 25–46</td></tr><tr><td valign="top">[a26]</td> <td valign="top"> S.P. Norton, "More on Moonshine" M.D. Atkinson (ed.) , ''Computational Group Theory'' , Acad. Press (1984) pp. 185–193</td></tr><tr><td valign="top">[a27]</td> <td valign="top"> A.P. Ogg, "Automorphismes des courbes modulaires" , ''Théorie des Nombres, Fasc. 1, Exp. 7, 8'' , ''Sém. Delange–Pisot–Poitou (16e année (1974/75)'' , Secr. Math. Paris (1975)</td></tr><tr><td valign="top">[a28]</td> <td valign="top"> L. Queen, "Modular functions arising from some finite groups" ''Math. Comp.'' , '''37''' : 156 (1981) pp. 547–580</td></tr><tr><td valign="top">[a29]</td> <td valign="top"> A.J.E. Ryba, "Modular Moonshine?" C. Dong (ed.) , ''Moonshine, the Monster, and related topics (South Hadley, MA, (1994)'' , ''Contemp. Math.'' , '''193''' , Amer. Math. Soc. (1996) pp. 307–336</td></tr><tr><td valign="top">[a30]</td> <td valign="top"> S.D. Smith, "On the head characters of the Monster simple group" , ''Finite groups: coming of age (Montreal, Que. 1982)'' , ''Contemp. Math.'' , '''45''' , Amer. Math. Soc. (1985) pp. 303–313</td></tr><tr><td valign="top">[a31]</td> <td valign="top"> J.G. Thompson, "Some numerology between the Fischer–Griess monster and the elliptic modular function" ''Bull. London Math. Soc.'' , '''11''' : 3 (1979) pp. 352–353</td></tr></table> |
Revision as of 17:42, 1 July 2020
According to the classification theorem, the simple finite groups (cf. also Simple finite group) consist of the cyclic groups of prime order (cf. also Cyclic group), the alternating groups of degree at least $5$ (cf. also Alternating group), the Chevalley and twisted Chevalley groups (cf. also Chevalley group), the Tits group and the $26$ sporadic simple groups (cf. also Sporadic simple group). The first five sporadic groups were described by E. Mathieu in the 19th century [a24], [a25]. No further sporadic groups were found until Z. Janko's discovery of the first modern sporadic group in 1964 [a14], [a15]. Evidence for the existence of the largest of the sporadic groups, $\mathcal{M}$, was found independently by B. Fischer and R.L. Griess in 1973. This group is now known as the monster and has order
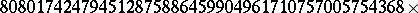 |
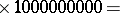 |
\begin{equation*} = 2 ^ { 46 } . 3 ^ { 20 } . 5 ^ { 9 } . 7 ^ { 6 } . 11 ^ { 2 } . 13 ^ { 3 }. \end{equation*}
\begin{equation*} .17.19 .23 .29 .31 .41 .47 .59 .71. \end{equation*}
Even before Griess's construction [a12] of $\mathcal{M}$ in 1981, intriguing connections between $\mathcal{M}$ and other areas of mathematics had been noted:
Define
\begin{equation*} \Gamma _ { 0 } ( N ) = \left\{ \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \in \operatorname{SL} ( 2 , \mathbf{Z} ) : c \equiv 0 ( \operatorname { mod } N ) \right\}, \end{equation*}
and for each prime number $p$, let $\Gamma _ { 0 } ( p ) + = \langle \Gamma _ { 0 } ( p ) , \left( \begin{array} { c c } { 0 } & { - 1 } \\ { p } & { 0 } \end{array} \right) \rangle$. Any discrete subgroup $G$ of $\operatorname{SL} ( 2 , \mathbf R )$ acts on the upper half of the complex plane by fractional-linear transformations (cf. also Fractional-linear mapping). The corresponding quotient space has the structure of a Riemann surface. If this surface is isomorphic to a sphere (with a finite number of points removed, corresponding to the orbits of the fixed points of the parabolic elements of $G$), then $G$ is said to have genus zero. In 1974, A.P. Ogg [a27] observed that the primes dividing the order of $\mathcal{M}$ are also the primes for which the group $\Gamma _ { 0 } ( p ) +$ has genus zero.
Suppose $G$ has genus zero; then a generator for the function field of $G$ is called a Hauptmodul. Suppose further that $G$ is commensurable with $\operatorname{SL} ( 2 , {\bf Z} )$ and that $G$ contains $z \mapsto z + k$ if and only if $k \in \mathbf{Z}$; then $G$ has a Hauptmodul of the form:
\begin{equation*} \frac { 1 } { q } + a _ { 0 } + a _ { 1 } q + a _ { 2 } q ^ { 2 } + \ldots , \quad q = \operatorname { exp } ( 2 \pi i z ). \end{equation*}
This form is unique except for the choice of $a_{0}$. For example $\operatorname{SL} ( 2 , {\bf Z} )$ has a Hauptmodul
\begin{equation*} J ( z ) = j ( z ) - 744 = \sum _ { k } c _ { k } q ^ { k } = \end{equation*}
\begin{equation*} = \frac { 1 } { q } + 196884 q + 21493760 q ^ { 2 } + 864299970 q ^ { 3 } + \end{equation*}
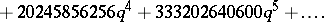 |
In 1978, J. McKay observed in a letter to J.G. Thompson that the coefficient $c_1$ is $196883 + 1$ and that 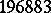 is the degree of the smallest non-trivial irreducible complex representation of $\mathcal{M}$. Thompson [a31] extended this observation by noting that the coefficients $a_1$, $a _2$, $a_3$, $a_4$, and $a_5$ of $J$ are simple linear combinations of the seven smallest irreducible degrees of $\mathcal{M}$. He also asked whether there exists a graded $\mathcal{M}$-module $V ^ { \natural } = \oplus _ { n } V _ { n }$, now known as the moonshine module, such that
is the degree of the smallest non-trivial irreducible complex representation of $\mathcal{M}$. Thompson [a31] extended this observation by noting that the coefficients $a_1$, $a _2$, $a_3$, $a_4$, and $a_5$ of $J$ are simple linear combinations of the seven smallest irreducible degrees of $\mathcal{M}$. He also asked whether there exists a graded $\mathcal{M}$-module $V ^ { \natural } = \oplus _ { n } V _ { n }$, now known as the moonshine module, such that
\begin{equation*} J ( z ) = \sum _ { n } \operatorname { Tr } ( e | _{V _ { n }} ) q ^ { n } \end{equation*}
where $e$ is the identity element of $\mathcal{M}$.
In 1979, J.H. Conway and S.P. Norton [a7] coined the term "moonshine" for the study of the links between modular functions and the sporadic simple groups (cf. also Modular group; Modular form; Modular function). They generalized the observations of McKay and Thompson by attaching to each element $g \in \mathcal{M}$ a genus-zero group $G _ { g }$, depending only on the conjugacy class of $g$, with Hauptmodul:
\begin{equation*} j_g ( z ) = \frac { 1 } { q } + a _ { 1 } ( g ) q + a _ { 2 } ( g ) q ^ { 2 } + \dots \end{equation*}
with $j _ { e } ( z ) = J ( z )$. The 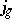 , $g \in \mathcal{M}$, are now known as the Thompson–McKay series. Conway and Norton conjectured that $\operatorname { Tr } ( g |_{ V _ n} ) = a _ { n } ( g )$, so that for each $n \geq - 1$ the mapping $g \mapsto a _ { n } ( g )$ defines a character $\mathcal{M}$ (cf. also Character of a group), which they called the $n$th Head character. They also conjectured identities between the Thompson–McKay series, which they called the replication identities:
, $g \in \mathcal{M}$, are now known as the Thompson–McKay series. Conway and Norton conjectured that $\operatorname { Tr } ( g |_{ V _ n} ) = a _ { n } ( g )$, so that for each $n \geq - 1$ the mapping $g \mapsto a _ { n } ( g )$ defines a character $\mathcal{M}$ (cf. also Character of a group), which they called the $n$th Head character. They also conjectured identities between the Thompson–McKay series, which they called the replication identities:
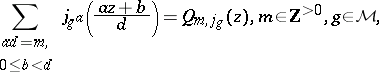 |
where $Q _ { m , j_g }$ is the unique polynomial in 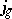 such that
such that
\begin{equation*} Q_{ m ,\, j_{ g} } - \frac { 1 } { q ^ { m } } \in q \mathbf{Z} [ [ q ] ]. \end{equation*}
These conjectures, and others contained in [a7], constitute the moonshine conjectures.
Given the character table of $\mathcal{M}$ (which was computed by B. Fischer, D. Livingstone and M.P. Thorne) and the Hauptmoduls  , $g \in \mathcal{M}$, Thompson observed that the mapping $g \mapsto a _ { n } ( g )$ is a virtual character of $\mathcal{M}$ for all $n$ if certain congruence conditions hold for a finite number of the $a_n ( g )$. He also showed that if $g \mapsto a _ { n } ( g )$ is a proper character for $\leq 1200$, then it is a proper character for all $n \geq 1$. Thus, in principle, the proof of the existence of $V ^ { \natural }$ can be reduced to a finite computation. Using these methods, A.O.L. Atkin, P. Fong and S.D. Smith [a10], [a30] showed that the Head characters are indeed virtual characters of $\mathcal{M}$ and gave very strong evidence that they are proper characters.
, $g \in \mathcal{M}$, Thompson observed that the mapping $g \mapsto a _ { n } ( g )$ is a virtual character of $\mathcal{M}$ for all $n$ if certain congruence conditions hold for a finite number of the $a_n ( g )$. He also showed that if $g \mapsto a _ { n } ( g )$ is a proper character for $\leq 1200$, then it is a proper character for all $n \geq 1$. Thus, in principle, the proof of the existence of $V ^ { \natural }$ can be reduced to a finite computation. Using these methods, A.O.L. Atkin, P. Fong and S.D. Smith [a10], [a30] showed that the Head characters are indeed virtual characters of $\mathcal{M}$ and gave very strong evidence that they are proper characters.
These calculations, however, did not give any information leading to a more conceptual understanding of $V ^ { \natural }$ and the moonshine conjectures. Another approach to $V ^ { \natural }$ was suggested by the explanations by J. Lepowsky [a20] and V.G. Kac [a16] of another observation of McKay that the coefficients of $j ^ { 1 / 3 }$ appear to be character degrees of the complex Lie group $E _ { 8 }$. The underlying structure in this case is that of the affine Kac–Moody Lie algebra $\hat { E } _ { 8 }$ (cf. also Kac–Moody algebra). The corresponding construction for $V ^ { \natural }$ was found by I. Frenkel, Lepowsky and A. Meurman [a11]. The additional structure is that of a vertex operator algebra. R.E. Borcherds [a2], [a5], [a17] defined a (real) vertex algebra to be a vector space $V$ with an infinite number of bilinear products $V \times V \rightarrow \mathbf{R}$, $( u , v ) \mapsto u _ { n } v$ for $u , v \in V$, $n \in \mathbf{Z}$, such that:
V.1) $u _ { n } v = 0$ for all $n$ sufficiently large (depending on $u$ and $v$);
V.2) (the "Jacobi identity" )
\begin{equation*} \sum _ { i \geq 0 } \left( \begin{array} { c } { m } \\ { i } \end{array} \right) ( u _ { q + i } v ) _ { m + n - i } w = \end{equation*}
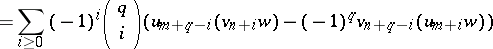 |
for all $u , v , w \in V$ and for all integers $m$, $n$ and $q$;
V.3) there is an element $1 \in V$ such that, for all $v \in V$, $v _ { n } 1 = 0$ if $n \geq 0$ and $v _{- 1}1 = v$. Also, $1 _ { - 1 } = \operatorname { id}$ (the identity transformation on $V$) and $1 _ { n } = 0$ for $n \neq - 1$.
A vertex operator algebra (VOA) is a vertex algebra which incorporates the action of the Virasoro Lie algebra (cf. also Virasoro algebra). Frenkel, Lepowsky and Meurman constructed $V ^ { \natural }$ as a vertex operator algebra of conformal dimension $24$. They made a crucial link between the vertex operator algebra structure of $V ^ { \natural }$ and Griess's construction of $\mathcal{M}$ via the Griess algebra and were thus able to show that $V ^ { \natural }$ is an $\mathcal{M}$-module. Their construction provides explicit formulas for the graded traces of elements of $\mathcal{M}$ which commute with an element in the class 2B (Atlas notation, cf. [a1]) in $\mathcal{M}$. For example, the corresponding formula for the $J$ function is:
\begin{equation*} J ( z ) = \end{equation*}
\begin{equation*} = \frac { 1 } { 2 } \left( \frac { \Theta _ { \Delta } ( q ) } { \eta ( q ) ^ { 24 } } + \frac { \eta ( q ) ^ { 24 } } { \eta ( q ^ { 2 } ) ^ { 24 } } \right) + \end{equation*}
\begin{equation*} + \frac { 1 } { 2 } \left( 2 ^ { 12 } \frac { \eta ^ { 24 } ( q ) } { \eta ( q ^ { 1 / 2 } ) ^ { 24 } } - 2 ^ { 12 } \frac { \eta ( q ^ { 2 } ) ^ { 24 } \eta ( q ^ { 1 / 2 } ) ^ { 24 } } { \eta ( q ) ^ { 48 } } \right), \end{equation*}
where $\Theta _ { \Lambda } ( q )$ is the theta-function of the Leech lattice $\Lambda$ and $\eta ( q ) = q ^ { 1 / 24 } \prod _ { i = 1 } ^ { \infty } ( 1 - q ^ { i } )$. In principle, this gives a case-by-case verification of the moonshine conjectures for these elements.
To complete the proof of the moonshine conjectures, Borcherds [a4] exploited the structure of $V ^ { \natural }$ to construct a Lie algebra, which he called the Monster Lie algebra. The construction also shows that the Monster Lie algebra is a generalized Kac–Moody Lie algebra (GKM Lie algebra), which is defined by Borcherds [a3] to be a Lie algebra $L$ such that:
1) $L$ has a $\bf Z$-grading $L = \oplus _ { n \in \mathbf{Z} } L _ { n }$ and $L_i$ is finite dimensional if $i \neq 0$;
2) $L$ has an involution $\omega$ such that $\omega : L _ { i } \rightarrow L _ { - i }$ and acts as $- 1$ on $L_0$;
3) $L$ has an invariant bilinear form $( \, . \, , \, . \, )$ such that:
a) $( \, . \, , \, . \, )$ is invariant under $\omega$;
b) $L_{ -i}$ and $L_{j}$ are orthogonal if $i \neq j$;
c) $- ( x , \omega ( x ) ) > 0$ if $x$ is a non-zero homogeneous element of $L$ of non-zero degree.
Remarkably, generalized Kac–Moody Lie algebras have many of the properties of Kac–Moody Lie algebras. In particular, they have "Weyl denominator" formulas, which in the case of the Monster Lie algebra is the product formula for the $j$-function:
\begin{equation*} p ^ { - 1 } \prod _ { \substack{m > 0 \\ n \in \mathbf{Z} } } ( 1 - p ^ { m } q ^ { n } ) ^ { c_{m n} } = j ( w ) - j ( z ) , p = \operatorname { exp } ( 2 \pi i w ) , \quad q = \operatorname { exp } ( 2 \pi i z ). \end{equation*}
The monster Lie algebra inherits an action of $\mathcal{M}$ from $V ^ { \natural }$, and so there are also "twisted" versions of the denominator formula, which can be interpreted as the denominator formulas of certain Lie superalgebras related to the Monster Lie algebra [a3]. Moreover, by the "no-ghost" theorem, which was first discovered in string theory [a3], [a13], these twisted versions of the denominator formula provide relations between the Thompson–McKay series of the moonshine module. These relations are exactly the replication identities conjectured by Conway and Norton.
One consequence of these identities is that each Thompson–McKay series satisfies certain recurrence relations. For the $j$-function these recurrences were first found by D.H. Lehmer [a19] and were rediscovered by K. Mahler [a21]. These relations determine ${ j}_g = 1 / q + a _ { 1 } ( g ) q +\dots$ if $a _ { 1 } ( g )$, $a _ { 2 } ( g )$, $a _ { 3 } ( g )$, $a_5 ( g )$ and $j _ { g } 2$ are known. In particular, if $g$ has odd order, then the coefficients of 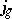 can be calculated once $a _ { 1 } ( g )$, $a _ { 2 } ( g )$, $a _ { 3 } ( g )$, $a_5 ( g )$ are known. The moonshine conjectures now follow from a calculation of the first $5$ coefficients of the Thompson–McKay series and the proof by M. Koike [a18] that the Hauptmoduls in question also satisfy the replication identities.
can be calculated once $a _ { 1 } ( g )$, $a _ { 2 } ( g )$, $a _ { 3 } ( g )$, $a_5 ( g )$ are known. The moonshine conjectures now follow from a calculation of the first $5$ coefficients of the Thompson–McKay series and the proof by M. Koike [a18] that the Hauptmoduls in question also satisfy the replication identities.
The original moonshine conjectures have been generalized in several directions and there has also been much work on the theory and applications of vertex operator algebras and generalized Kac–Moody Lie algebras. A far from complete list is: Norton's replicable functions [a26] and generalized moonshine conjectures [a23], [a8]; moonshine for other groups [a22], [a28]; A.J.E. Ryba's modular moonshine conjectures [a29], [a4], [a6] and the development of the general theory of vertex operator algebras [a9].
References
| [a1] | J.H. Conway, R.T. Curtis, S.P. Norton, R.A. Parker, R.A. Wilson, "Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J.G. Thackray" , Oxford Univ. Press (1985) |
| [a2] | R.E. Borcherds, "Vertex algebras, Kac–Moody algebras, and the Monster" Proc. Nat. Acad. Sci. USA , 83 (1986) pp. 3068–3071 |
| [a3] | R.E. Borcherds, "Monstrous Moonshine and monstrous Lie superalgebras" Invent. Math. , 109 (1992) pp. 405–444 |
| [a4] | R.E. Borcherds, "Modular moonshine. III" Duke Math. J. , 93 (1998) pp. 129–154 |
| [a5] | R.E. Borcherds, "Generalized Kac–Moody algebras" J. Algebra , 115 (1988) pp. 501–512 |
| [a6] | R.E. Borcherds, A.J.E. Ryba, "Modular Moonshine. II" Duke Math. J. , 83 (1996) pp. 435–459 |
| [a7] | J.H. Conway, S.P. Norton, "Monstrous Moonshine" Bull. London Math. Soc. , 11 (1979) pp. 308–339 |
| [a8] | C. Dong, H. Li, G. Mason, "Modular invariance of trace functions in orbifold theory" preprint (1997) |
| [a9] | C. Dong, G. Mason, "Vertex operator algebras and Moonshine: a survey" , Progress in Algebraic Combinatorics (Fukuoka, 1993) , Adv. Stud. Pure Math. , 24 , Math. Soc. Japan (1996) pp. 101–136 |
| [a10] | P. Fong, "Characters arising in the Monster-modular connection" , The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979 , Proc. Symp. Pure Math. , 37 , Amer. Math. Soc. (1980) pp. 557–559 |
| [a11] | I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operators and the monster" , Acad. Press (1988) |
| [a12] | R.L. Griess, "The friendly giant" Invent. Math. , 69 (1982) pp. 1–102 |
| [a13] | P. Goddard, C.B. Thorne, "Compatibility of the dual Pomeron with unitarity and the absence of ghosts in the dual resonance model" Phys. Lett. B , 40 (1972) pp. 235–238 |
| [a14] | Z. Janko, "A new finite simple group with abelian $2$-Sylow subgroups" Proc. Nat. Acad. Sci. USA , 53 (1965) pp. 657–658 |
| [a15] | Z. Janko, "A new finite simple group with abelian Sylow $2$-subgroups and its characterization" J. Algebra , 3 (1966) pp. 147–186 |
| [a16] | V.G. Kac, "An elucidation of: Infinite-dimensional algebras, Dedekind's $ \eta $-function, classical Möbius function and the very strange formula $E _ { 8 } ^ { ( 1 ) }$ and the cube root of the modular invariant $j$" Adv. Math. , 35 : 3 (1980) pp. 264–273 |
| [a17] | V.G. Kac, "Vertex algebras for beginners" , Univ. Lecture Ser. , 10 , Amer. Math. Soc. (1997) |
| [a18] | M. Koike, "On replication formula and Hecke operators" Preprint Nagoya Univ. (unpublished) |
| [a19] | D.H. Lehmer, "Properties of the coefficients of the modular invariant $J ( \tau )$" Amer. J. Math. , 64 (1942) pp. 488–502 |
| [a20] | J. Lepowsky, "Euclidean Lie algebras and the modular function $j$" , The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979) , Proc. Symp. Pure Math. , 37 , Amer. Math. Soc. (1980) pp. 567–570 |
| [a21] | K. Mahler, "On a class of non-linear functional equations connected with modular functions" J. Austral. Math. Soc. , 22A (1976) pp. 65–118 |
| [a22] | G. Mason, "$M _ { 24 }$ and certain automorphic forms" , Finite groups: coming of age (Montreal, Que., 1982) , Contemp. Math. , 45 , Amer. Math. Soc. (1985) pp. 223–244 |
| [a23] | G. Mason, "Finite groups and modular functions" , The Arcata Conference on Representations of Finite Groups (Arcata, Calif. 1986) , Proc. Symp. Pure Math. , 47:1 , Amer. Math. Soc. (1987) pp. 181–210 (Appendix by S.P. Norton) |
| [a24] | E. Mathieu, "Memoire sur l'étude des fonctions de plusieurs quantités" J. Math. Pures Appl. , 6 (1861) pp. 241–323 |
| [a25] | E. Mathieu, "Sur les fonctions cinq fois transitives de $24$ quantités" J. Math. Pures Appl. , 18 (1873) pp. 25–46 |
| [a26] | S.P. Norton, "More on Moonshine" M.D. Atkinson (ed.) , Computational Group Theory , Acad. Press (1984) pp. 185–193 |
| [a27] | A.P. Ogg, "Automorphismes des courbes modulaires" , Théorie des Nombres, Fasc. 1, Exp. 7, 8 , Sém. Delange–Pisot–Poitou (16e année (1974/75) , Secr. Math. Paris (1975) |
| [a28] | L. Queen, "Modular functions arising from some finite groups" Math. Comp. , 37 : 156 (1981) pp. 547–580 |
| [a29] | A.J.E. Ryba, "Modular Moonshine?" C. Dong (ed.) , Moonshine, the Monster, and related topics (South Hadley, MA, (1994) , Contemp. Math. , 193 , Amer. Math. Soc. (1996) pp. 307–336 |
| [a30] | S.D. Smith, "On the head characters of the Monster simple group" , Finite groups: coming of age (Montreal, Que. 1982) , Contemp. Math. , 45 , Amer. Math. Soc. (1985) pp. 303–313 |
| [a31] | J.G. Thompson, "Some numerology between the Fischer–Griess monster and the elliptic modular function" Bull. London Math. Soc. , 11 : 3 (1979) pp. 352–353 |
Thompson-McKay series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thompson-McKay_series&oldid=35120