Thomas-Fermi theory
Fermi–Thomas theory
Sometimes called the
"statistical theory" ,
it was invented by
L.H. Thomas
and
E. Fermi
[a2],
shortly after
E. Schrödinger
invented his
quantum-mechanical wave equation, in order to approximately
describe the
electron density,
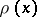 ,
,
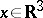 ,
,
and the
ground state energy,

for a large atom or molecule with a large number,
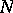 ,
,
of electrons. Schrödinger's
equation, which would give the exact density and energy, cannot be
easily handled when
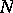
is large (cf. also
A starting point for the theory is the
Thomas–Fermi energy functional.
For a molecule with
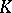
nuclei of charges
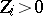
and locations
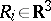
(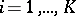 ),
),
it is
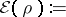 | (a1) |
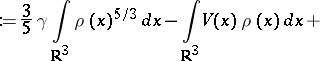 |
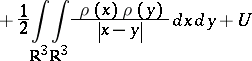 |
in suitable units. Here,
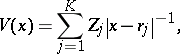 |
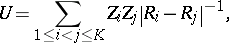 |
and
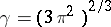 .
.
The constraint on
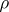
is
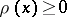
and
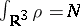 .
.
The functional
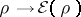
is convex (cf. also
Convex function (of a real variable)).
The justification for this functional is this:
The first term is roughly the minimum quantum-mechanical
kinetic energy of
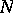
electrons needed to produce an electron density
 .
.
The second term is the attractive interaction of the
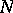
electrons with the
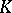
nuclei, via the
Coulomb potential
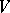 .
.
The third is approximately the electron-electron repulsive
energy.
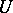
is the nuclear-nuclear repulsion and is an important constant.
The
Thomas–Fermi energy
is defined to be
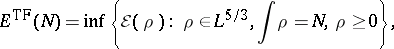 |
i.e., the Thomas–Fermi energy and density are obtained by minimizing
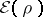
with
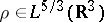
and
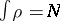 .
.
The
in this case called the
Thomas–Fermi equation,
is
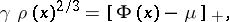 | (a2) |
where
 ,
,
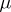
is some constant
(a
Lagrange multiplier; cf.
and
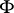
is the
Thomas–Fermi potential:
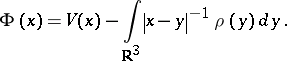 | (a3) |
The following essential mathematical facts about the
Thomas–Fermi equation were
established by
E.H. Lieb
and
B. Simon
(cf. also
[a3]):
1)
There is a density
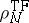
that minimizes
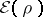
if and only if
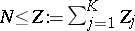 .
.
This
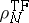
is unique and it satisfies the Thomas–Fermi equation
(a2)
for some
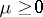 .
.
Every positive solution,
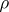 ,
,
of
(a2)
is a minimizer of
(a1)
for
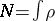 .
.
If
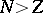 ,
,
then
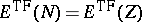
and any minimizing sequence converges weakly in
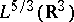
to
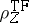 .
.
2)
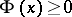
for all
 .
.
(This need not be so for the real Schrödinger
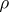 .)
.)
3)
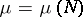
is a strictly monotonically decreasing function of
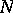
and
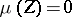
(the
neutral case).
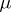
is the
chemical potential,
namely
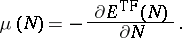 |
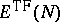
is a strictly convex, decreasing function of
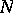
for
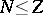
and
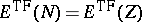
for
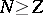 .
.
If
 ,
,
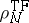
has compact support.
When
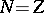 ,
,
(a2)
becomes
 .
.
By applying the
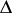
to both sides, one obtains
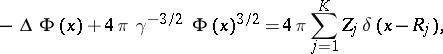 |
which is the form in which the Thomas–Fermi
equation is usually stated (but it
is valid only for
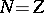 ).
).
An important property of the solution is
Teller's theorem
(proved rigorously in
[a7]),
which implies that the
Thomas–Fermi molecule
is always unstable, i.e., for each
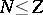
there are
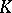
numbers
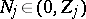
with
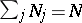
such that
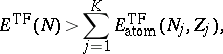 | (a4) |
where
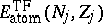
is the Thomas–Fermi
energy with
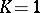 ,
,
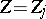
and
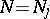 .
.
The presence of
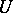
in
(a1)
is crucial for this result. The inequality is strict. Not only does
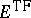
decrease when the nuclei are pulled infinitely far apart (which is
what
(a4)
says) but any dilation of the nuclear coordinates
( ,
,
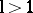 )
)
will decrease
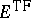
in the neutral case
(positivity of the pressure)
[a3],
[a1].
This theorem plays an important role in the
stability of matter.
An important question concerns the connection between
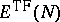
and
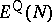 ,
,
the
ground state energy
(i.e., the infimum of the spectrum) of the
Schrödinger operator,
 ,
,
it was meant to approximate.
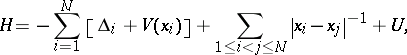 |
which acts on the
anti-symmetric functions
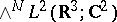
(i.e., functions of space and spin). It used to be believed that
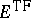
is asymptotically exact as
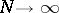 ,
,
but this is not quite right;
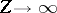
is also needed.
Lieb
and
Simon
proved that if one fixes
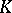
and
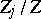
and sets
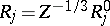 ,
,
with fixed
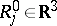 ,
,
and sets
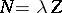 ,
,
with
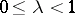 ,
,
then
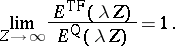 | (a5) |
In particular, a simple change of variables shows that
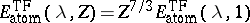
and hence the true energy of a large atom is asymptotically
proportional to
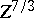 .
.
Likewise, there is a well-defined sense in which the
quantum-mechanical density converges to
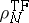
(cf.
[a7]).
The Thomas–Fermi density for an atom located at
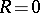 ,
,
which is spherically symmetric, scales as
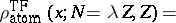 |
 |
Thus, a large atom (i.e., large
 )
)
is smaller than a
atom by a factor
in radius. Despite this seeming paradox, Thomas–Fermi
theory gives the correct
electron density in a real atom (so far as the bulk of the
electrons is concerned) as
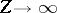 .
.
Another important fact is the
large-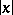
asymptotics of
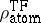
for a neutral atom. As
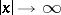 ,
,
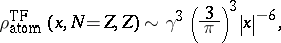 |
independent of
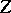 .
.
Again, this behaviour agrees with quantum mechanics — on a
length scale
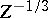 ,
,
which is where the bulk of the electrons is to be found.
In light of the limit theorem
(a5),
Teller's theorem
can be understood as saying that, as
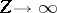 ,
,
the quantum-mechanical binding energy of a molecule is of lower order
in
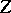
than the total ground state energy. Thus, Teller's theorem is
not a defect of Thomas–Fermi
theory (although it is sometimes interpreted that
way) but an important statement about the true quantum-mechanical
situation.
For finite
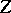
one can show, using the
and the
Lieb–Oxford inequality
[a6],
that
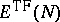 ,
,
with a modified
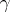 ,
,
gives a lower bound to
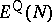 .
.
Several
"improvements"
to Thomas–Fermi theory have been proposed, but none have a
fundamental significance in the sense of being
"exact"
in the

limit. The
von Weizsäcker correction
consists in adding a term
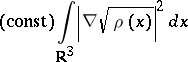 |
to
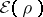 .
.
This preserves the convexity of
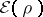
and adds

to
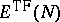
when
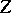
is large. It also has the effect that the range of
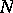
for which there is a minimizing
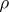
is extend from
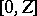
to
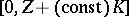 .
.
Another correction, the
Dirac exchange energy,
is to add
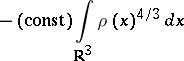 |
to
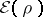 .
.
This spoils the convexity but not the range
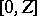
for which a
minimizing
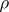
exists, cf.
for both of these corrections.
When a uniform external magnetic field

is present, the operator
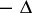
in
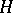
is replaced by
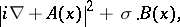 |
with
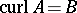
and
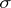
denoting the Pauli spin matrices (cf. also
This leads to a modified Thomas–Fermi theory
that is asymptotically exact as
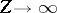 ,
,
but the theory depends on the manner in which
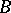
varies with
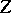 .
.
There are five distinct regimes and theories:
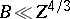 ,
,
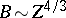 ,
,
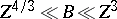 ,
,
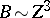 ,
,
and
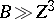 .
.
These
theories
[a8],
are relevant for
neutron stars.
Another class of Thomas–Fermi theories with
magnetic fields is relevant for electrons confined to
two-dimensional geometries
(quantum dots)
In this case there are three regimes. A convenient review
is
Still another modification of Thomas–Fermi theory
is its extension from a
theory of the ground states of atoms and molecules (which corresponds
to zero temperature) to a theory of positive temperature states of
large systems such as stars
(cf.
[a5],
[a14]).
References
| [a1] |
R. Benguria, E.H. Lieb, "The positivity of the pressure in Thomas–Fermi theory" Comm. Math. Phys. , 63 (1978) pp. 193–218 ((Errata: 71 (1980), 94)) |
| [a2] |
E. Fermi, "Un metodo statistico per la determinazione di alcune priorieta dell'atome" Rend. Accad. Naz. Lincei , 6 (1927) pp. 602–607 |
| [a3] |
E.H. Lieb, "Thomas–Fermi and related theories of atoms and molecules" Rev. Mod. Phys. , 53 (1981) pp. 603–641 ((Errata: 54 (1982), 311)) |
| [a4] |
E. Teller, "On the stability of molecules in Thomas–Fermi theory" Rev. Mod. Phys. , 34 (1962) pp. 627–631 |
| [a5] |
J. Messer, "Temperature dependent Thomas–Fermi theory" , Lecture Notes Physics , 147 , Springer (1981) |
| [a6] |
E.H. Lieb, S. Oxford, "An improved lower bound on the indirect Coulomb energy" Internat. J. Quant. Chem. , 19 (1981) pp. 427–439 |
| [a7] |
E.H. Lieb, B. Simon, "The Thomas–Fermi theory of atoms, molecules and solids" Adv. Math. , 23 (1977) pp. 22–116 |
| [a8] |
E.H. Lieb, J.P. Solovej, J. Yngvason, "Asymptotics of heavy atoms in high magnetic fields: I. lowest Landau band region" Commun. Pure Appl. Math. , 47 (1994) pp. 513–591 |
| [a9] |
E.H. Lieb, J.P. Solovej, J. Yngvason, "Asymptotics of heavy atoms in high magnetic fields: II. semiclassical regions" Comm. Math. Phys. , 161 (1994) pp. 77–124 |
| [a10] |
E.H. Lieb, J.P. Solovej, J. Yngvason, "Ground states of large quantum dots in magnetic fields" Phys. Rev. B , 51 (1995) pp. 10646–10665 |
| [a11] |
E.H. Lieb, J.P. Solovej, J. Yngvason, "Asymptotics of natural and artificial atoms in strong magnetic fields" W. Thirring (ed.) , The stability of matter: from atoms to stars, selecta of E.H. Lieb , Springer (1997) pp. 145–167 (Edition: Second) |
| [a12] |
E.H. Lieb, W. Thirring, "Inequalities for the moments of the eigenvalues of the Schrödinger Hamiltonian and their relation to Sobolev inequalities" E. Lieb (ed.) B. Simon (ed.) A. Wightman (ed.) , Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann , Princeton Univ. Press (1976) pp. 269–303 ((See also: W. Thirring (ed.), The stability of matter: from the atoms to stars, Selecta of E.H. Lieb, Springer, 1977)) |
| [a13] |
L.H. Thomas, "The calculation of atomic fields" Proc. Cambridge Philos. Soc. , 23 (1927) pp. 542–548 |
| [a14] |
W. Thirring, "A course in mathematical physics" , 4 , Springer (1983) pp. 209–277 |
Elliott H. Lieb
Copyright to this article is held by Elliott Lieb.
Thomas-Fermi theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thomas-Fermi_theory&oldid=15593