Thom class
An element in the (generalized) cohomology group of a Thom space, generating it as a module over the cohomology ring of the base space. For a multiplicative generalized cohomology theory (cf. Generalized cohomology theories)  , let
, let  be the image of
be the image of  under the
under the  -fold suspension isomorphism
-fold suspension isomorphism  . Let
. Let  be an
be an  -dimensional vector bundle over a path-connected finite cell complex
-dimensional vector bundle over a path-connected finite cell complex  , and let
, and let  be the corresponding inclusion into the Thom space. An element
be the corresponding inclusion into the Thom space. An element  is called a Thom class (or orientation) of the bundle
is called a Thom class (or orientation) of the bundle  if
if  , with
, with  invertible in
invertible in  . A bundle need not have a Thom class. A bundle with a Thom class (in
. A bundle need not have a Thom class. A bundle with a Thom class (in 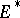 ) is called
) is called 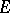 -orientable, and a bundle with a fixed Thom class is
-orientable, and a bundle with a fixed Thom class is  -oriented. The number of Thom classes of an
-oriented. The number of Thom classes of an  -orientable bundle over
-orientable bundle over  is equal to the number of elements of the group
is equal to the number of elements of the group  . Multiplication by a Thom class gives a Thom isomorphism.
. Multiplication by a Thom class gives a Thom isomorphism.
Comments
For a (topological) manifold with or without boundary 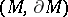 , a Thom class is a Thom class for its tangent (micro) bundle. Given a Thom class
, a Thom class is a Thom class for its tangent (micro) bundle. Given a Thom class 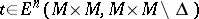 , there are isomorphisms
, there are isomorphisms 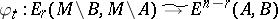 (Alexander duality),
(Alexander duality), 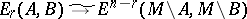 ,
,  (Lefschetz duality) and
(Lefschetz duality) and  ,
,  (Poincaré duality), where
(Poincaré duality), where  is a compact triangulable manifold and
is a compact triangulable manifold and  are compact subpolyhedra, cf. [a1], Chapt. 14, for more details.
are compact subpolyhedra, cf. [a1], Chapt. 14, for more details.
An element  is called a fundamental class if for every
is called a fundamental class if for every 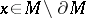 one has that
one has that  (
(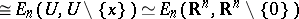 ) is a generator of
) is a generator of  as a module over
as a module over  . (Here
. (Here 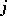 is the inclusion
is the inclusion 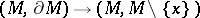 .) For the case of ordinary homology, cf. Fundamental class. The relation between a fundamental class and a Thom class is given by the result that if
.) For the case of ordinary homology, cf. Fundamental class. The relation between a fundamental class and a Thom class is given by the result that if 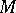 is a compact triangulable
is a compact triangulable  -manifold with Thom class
-manifold with Thom class 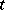 , then there is a unique fundamental class
, then there is a unique fundamental class  such that
such that  takes
takes  to
to 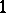 , cf. [a1], Prop. 14.17. Using this the Lefschetz and Poincaré duality isomorphisms defined by the Thom class
, cf. [a1], Prop. 14.17. Using this the Lefschetz and Poincaré duality isomorphisms defined by the Thom class  (which essentially are defined by a slant product with
(which essentially are defined by a slant product with  ) are given by a cap product with
) are given by a cap product with  .
.
References
| [a1] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapt. 2 |
Thom class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom_class&oldid=14266