Theodorsen integral equation
Theodorsen's integral equation [a7] is a well-known tool for computing numerically the conformal mapping  of the unit disc
of the unit disc  onto a star-like region
onto a star-like region  given by the polar coordinates
given by the polar coordinates  ,
,  of its boundary
of its boundary  . The mapping
. The mapping  is assumed to be normalized by
is assumed to be normalized by  ,
,  . It is uniquely determined by its boundary correspondence function
. It is uniquely determined by its boundary correspondence function 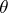 , which is implicitly defined by
, which is implicitly defined by
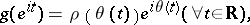 |
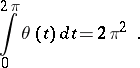 |
Theodorsen's equation follows from the fact that the function 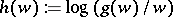 is analytic in
is analytic in 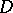 and can be extended to a homeomorphism of the closure
and can be extended to a homeomorphism of the closure  onto the closure
onto the closure  . It simply states that the
. It simply states that the 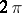 -periodic function
-periodic function 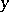 :
:  is the conjugate periodic function of
is the conjugate periodic function of  :
: 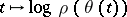 , that is,
, that is, 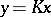 , where
, where 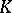 is the conjugation operator defined on
is the conjugation operator defined on 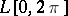 by the principal value integral
by the principal value integral
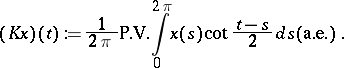 |
When restricted to 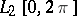 ,
,  is a skew-symmetric endomorphism of norm
is a skew-symmetric endomorphism of norm 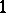 with a very simple diagonal representation in Fourier space: when
with a very simple diagonal representation in Fourier space: when  has the real Fourier coefficients
has the real Fourier coefficients  ,
, 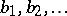 , then
, then 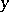 has the coefficients
has the coefficients 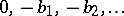 ,
,  .
.
Hence, while Theodorsen's integral equation is normally written as
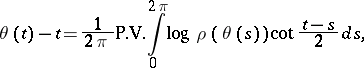 |
for practical purposes the conjugation is executed by transformation to Fourier space:  is approximated by a trigonometric polynomial of degree
is approximated by a trigonometric polynomial of degree  , whose Fourier coefficients are quickly found by the fast Fourier transform, which then can also be applied to determine values at
, whose Fourier coefficients are quickly found by the fast Fourier transform, which then can also be applied to determine values at 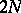 equi-spaced points of the trigonometric polynomial that approximates
equi-spaced points of the trigonometric polynomial that approximates  (cf. also Fourier series). Before the fast Fourier transform became the standard tool for this discrete conjugation process, the transition from the values of
(cf. also Fourier series). Before the fast Fourier transform became the standard tool for this discrete conjugation process, the transition from the values of  to those of
to those of 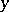 was based on multiplication by a matrix, called the Wittich matrix in [a1]. The fast Fourier transform meant a cost reduction from
was based on multiplication by a matrix, called the Wittich matrix in [a1]. The fast Fourier transform meant a cost reduction from 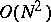 to
to  operations per iteration.
operations per iteration.
Until the end of the 1970s the recommendation was to solve a so-obtained discrete version of Theodorsen's equation by fixed-point (Picard) iteration, an approach that is limited to Jordan regions with piecewise differentiable boundary satisfying  , and is very slow when the bound
, and is very slow when the bound 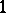 is nearly attained. Other regions, like those from airfoil design, which was the standard application targeted by T. Theodorsen, could be handled by using first a suitable preliminary conformal mapping, which turned the exterior of the wing cross-section into the exterior of a Jordan curve that is close to a circle; see [a6], Chapt. 10. Moreover, for this application, the equation has to be modified slightly to map the exterior of the disc onto the exterior of a Jordan curve.
is nearly attained. Other regions, like those from airfoil design, which was the standard application targeted by T. Theodorsen, could be handled by using first a suitable preliminary conformal mapping, which turned the exterior of the wing cross-section into the exterior of a Jordan curve that is close to a circle; see [a6], Chapt. 10. Moreover, for this application, the equation has to be modified slightly to map the exterior of the disc onto the exterior of a Jordan curve.
M. Gutknecht [a4], [a2] extended the applicability of Theodorsen's equation by applying more refined iterative methods and discretizations, and O. Hübner [a5] improved the convergence order from linear to quadratic by adapting R. Wegmann's treatment of a similar equation obtained by choosing  instead. Wegmann's method [a9], [a10] applies the Newton method and solves the linear equation for the corrections by interpreting it as a Riemann–Hilbert problem that can be solved with four fast Fourier transforms.
instead. Wegmann's method [a9], [a10] applies the Newton method and solves the linear equation for the corrections by interpreting it as a Riemann–Hilbert problem that can be solved with four fast Fourier transforms.
A common framework for conformal mapping methods based on function conjugation is given in [a3]; Theodorsen's restriction to regions given in polar coordinates can be lifted. Both Theodorsen's [a8] and Wegmann's [a11] equations and methods can be extended to the doubly connected case.
References
| [a1] | D. Gaier, "Konstruktive Methoden der konformen Abbildung" , Springer (1964) |
| [a2] | M.H. Gutknecht, "Numerical experiments on solving Theodorsen's integral equation for conformal maps with the fast Fourier transform and various nonlinear iterative methods" SIAM J. Sci. Statist. Comput. , 4 (1983) pp. 1–30 |
| [a3] | M.H. Gutknecht, "Numerical conformal mapping methods based on function conjugation" J. Comput. Appl. Math. , 14 (1986) pp. 31–77 |
| [a4] | M.H. Gutknecht, "Solving Theodorsen's integral equation for conformal maps with the fast Fourier transform and various nonlinear iterative methods" Numer. Math. , 36 (1981) pp. 405–429 |
| [a5] | O. Hübner, "The Newton method for solving the Theodorsen equation" J. Comput. Appl. Math. , 14 (1986) pp. 19–30 |
| [a6] | P.K. Kythe, "Computational conformal mapping" , Birkhäuser (1998) |
| [a7] | T. Theodorsen, "Theory of wing sections of arbitrary shape" Rept. NACA , 411 (1931) |
| [a8] | T. Theodorsen, I.E. Garrick, "General potential theory of arbitrary wing sections" Rept. NACA , 452 (1933) |
| [a9] | R. Wegmann, "Ein Iterationsverfahren zur konformen Abbildung" Numer. Math. , 30 (1978) pp. 453–466 |
| [a10] | R. Wegmann, "An iterative method for conformal mapping" J. Comput. Appl. Math. , 14 (1986) pp. 7–18 (Translated from German) (English translation of [9]) |
| [a11] | R. Wegmann, "An iterative method for the conformal mapping of doubly connected regions" J. Comput. Appl. Math. , 14 (1986) pp. 79–98 |
Theodorsen integral equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Theodorsen_integral_equation&oldid=15961