Tetracyclic coordinates
of a point in the plane
A kind of homogeneous coordinates  for a point
for a point  in the complex inversive plane. The numbers
in the complex inversive plane. The numbers  , not all zero, are connected by the relation
, not all zero, are connected by the relation
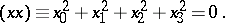 |
All points  which satisfy a linear equation
which satisfy a linear equation
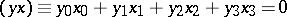 |
are said to form a circle with "coordinates"  . Two circles
. Two circles  and
and  are orthogonal if
are orthogonal if  , tangent if
, tangent if
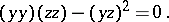 |
If two circles  and
and  intersect, the expression
intersect, the expression
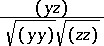 |
measures the cosine of their angle (or the hyperbolic cosine of their inversive distance).
In three dimensions, with an extra coordinate 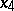 , one obtains the analogous pentaspherical coordinates, which lead to spheres instead of circles.
, one obtains the analogous pentaspherical coordinates, which lead to spheres instead of circles.
According to an alternative definition, involving only real numbers, tetracyclic coordinates of points and circles in the plane can be introduced using stereographic projection. Here the tetracyclic coordinates of a point in the plane are the homogeneous coordinates of the point on the sphere corresponding to it under stereographic projection. The tetracyclic coordinates of a circle in the plane are the homogeneous coordinates of the point in space that is the pole of the plane of the circle on the sphere which corresponds to the circle in the plane under stereographic projection with respect to that sphere.
Comments
The inversive plane, also called conformal plane, is obtained by adding an ideal point "∞" at infinity to the plane. The name derives from the fact that with this point added, inversion in a circle becomes an everywhere well-defined "automorphism" of period  . (Given a circle of radius
. (Given a circle of radius  and centre
and centre  , two points
, two points  and
and 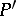 correspond under inversion in this circle if and only if
correspond under inversion in this circle if and only if 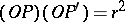 .) In the inversive plane all lines pass through
.) In the inversive plane all lines pass through  and a line (of the original plane) is a circle with centre at
and a line (of the original plane) is a circle with centre at  . Now all circles (lines) either touch or have two points of intersection.
. Now all circles (lines) either touch or have two points of intersection.
Inversive space (conformal space) is obtained by adding an ideal point at infinity to  -space (making inversion in a sphere everywhere well-defined of period
-space (making inversion in a sphere everywhere well-defined of period  ).
).
Any angle inverts into an equal angle, whence the terms "conformal space" and "conformal plane" for inversive space and inversive plane.
References
| [a1] | W.K. Clifford, "On the powers of spheres" , Mathematical Papers , Macmillan (1882) pp. 332–336 |
| [a2] | G. Darboux, "Sur les rélations entre les groupes de points, de circles et de sphères dans le plan et dans l'espace" Ann. Ecole Norm. Sup. , 1 (1872) pp. 323–392 |
| [a3] | F. Klein, "Vorlesungen über höhere Geometrie" , Chelsea, reprint (1949) |
| [a4] | R. Lachlan, "On systems of circles and spheres" Philos. Trans. Royal Soc. London A , 177 (1886) pp. 481–625 |
| [a5] | J.L. Coolidge, "A treatise on the circle and the sphere" , Clarendon Press (1916) |
| [a6] | F.G. Woods, "Higher geometry" , Ginn (1922) |
| [a7] | J.B. Wilker, "Inversive geometry" C. Davis (ed.) B. Grünbaum (ed.) F.A. Sherk (ed.) , The geometric vein (Coxeter-Festschrift) , Springer (1980) pp. 374–442 |
| [a8] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1969) pp. §6.4, §6.8 |
Tetracyclic coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tetracyclic_coordinates&oldid=31750