Tensor bundle
of type  on a differentiable manifold
on a differentiable manifold 
The vector bundle  over
over  associated with the bundle of tangent frames and having as standard fibre the space
associated with the bundle of tangent frames and having as standard fibre the space  of tensors (cf. Tensor on a vector space) of type
of tensors (cf. Tensor on a vector space) of type  on
on  , on which the group
, on which the group  acts by the tensor representation. For instance,
acts by the tensor representation. For instance, 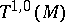 coincides with the tangent bundle
coincides with the tangent bundle  over
over  , while
, while 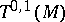 coincides with the cotangent bundle
coincides with the cotangent bundle 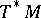 . In the general case, the tensor bundle is isomorphic to the tensor product of the tangent and cotangent bundles:
. In the general case, the tensor bundle is isomorphic to the tensor product of the tangent and cotangent bundles:
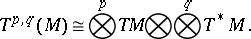 |
Sections of the tensor bundle of type 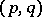 are called tensor fields of type
are called tensor fields of type 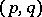 and are the basic object of study in differential geometry. For example, a Riemannian structure on
and are the basic object of study in differential geometry. For example, a Riemannian structure on 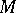 is a smooth section of the bundle
is a smooth section of the bundle  the values of which are positive-definite symmetric forms. The smooth sections of the bundle
the values of which are positive-definite symmetric forms. The smooth sections of the bundle  form a module
form a module 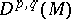 over the algebra
over the algebra  of smooth functions on
of smooth functions on 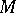 . If
. If 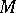 is a paracompact Hausdorff manifold, then
is a paracompact Hausdorff manifold, then
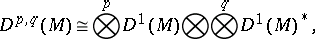 |
where  is the module of smooth vector fields,
is the module of smooth vector fields, 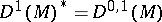 is the module of Pfaffian differential forms (cf. also Pfaffian form), and the tensor products are taken over
is the module of Pfaffian differential forms (cf. also Pfaffian form), and the tensor products are taken over 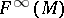 . In classical differential geometry tensor fields are sometimes simply called tensors on
. In classical differential geometry tensor fields are sometimes simply called tensors on  .
.
References
| [1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) |
| [2] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Comments
The space  of vector fields is often denoted by
of vector fields is often denoted by  , and
, and  , the space of Pfaffian forms, by
, the space of Pfaffian forms, by 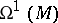 .
.
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Tensor bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tensor_bundle&oldid=17758