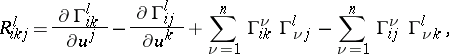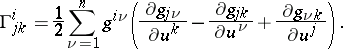A generalization of vector analysis, a part of tensor calculus studying differential (and integration) operators on the algebra 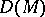 of differentiable tensor fields over a differentiable manifold
of differentiable tensor fields over a differentiable manifold  . Also the extension of this theory to more general geometric objects than tensor fields, such as tensor densities, vector-valued differential forms, etc. is considered as a part of tensor analysis.
. Also the extension of this theory to more general geometric objects than tensor fields, such as tensor densities, vector-valued differential forms, etc. is considered as a part of tensor analysis.
References
| [1] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | J.A. Schouten, "Tensor analysis for physicists" , Cambridge Univ. Press (1951) |
| [3] | A.J. MacConnel, "Applications of tensor analysis" , Dover, reprint (1957) |
| [4] | I.S. Sokolnikoff, "Tensor analysis" , Wiley (1964) |
The most important operators of tensor analysis map tensor fields into tensor fields, possibly changing the type of the field.
1) The covariant derivative in the direction of a vector field  is a linear mapping
is a linear mapping 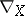 of the vector space
of the vector space 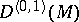 into itself satisfying the following conditions:
into itself satisfying the following conditions:
where 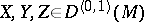 and
and 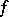 and
and 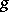 are smooth functions on
are smooth functions on 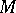 . In this interpretation the vector field
. In this interpretation the vector field 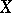 is considered as a derivation on functions, i.e. in local coordinates
is considered as a derivation on functions, i.e. in local coordinates 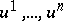 with
with 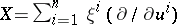 , for the derivative of the function
, for the derivative of the function 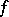 one has
one has 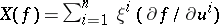 . The prescription of such an operator
. The prescription of such an operator 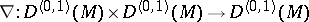 defines a linear connection and a parallel displacement along curves on
defines a linear connection and a parallel displacement along curves on 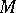 .
.
The extension of the covariant derivative to arbitrary tensor fields on 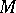 can be characterized by the properties that it is a derivation preserving the type of the tensor field and commuting with contraction. Regarding a tensor field of type
can be characterized by the properties that it is a derivation preserving the type of the tensor field and commuting with contraction. Regarding a tensor field of type 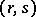 as a field of multilinear mappings which are defined on
as a field of multilinear mappings which are defined on  copies of the corresponding tangent space and
copies of the corresponding tangent space and  copies of the cotangent space, this extension is defined for
copies of the cotangent space, this extension is defined for 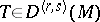 as follows:
as follows:
where 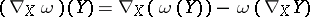 ,
, 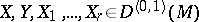 and
and 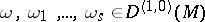 . This implies in local coordinates, using the notations introduced above and the connection coefficients
. This implies in local coordinates, using the notations introduced above and the connection coefficients 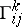 given by
given by 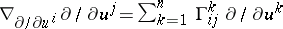 , the following formula in terms of the components
, the following formula in terms of the components 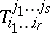 of
of 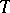 :
:
From this definition one easily obtains the covariant differential 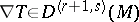 of the tensor field
of the tensor field 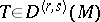 by
by
where the tensorial character of the first entry can be seen from the rules for  presented above. In the case of the Levi-Civita connection of a Riemannian metric on
presented above. In the case of the Levi-Civita connection of a Riemannian metric on 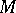 , the trace of the covariant differential of
, the trace of the covariant differential of 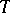 with respect to the first and some other covariant entry leads to an extension of the divergence to tensor fields.
with respect to the first and some other covariant entry leads to an extension of the divergence to tensor fields.
2) The Lie derivative along a vector field 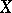 is the mapping
is the mapping 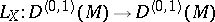 defined by
defined by 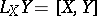 , where
, where 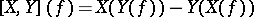 for any smooth function
for any smooth function 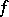 on
on 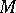 . The extension of the Lie derivative to arbitrary tensor fields
. The extension of the Lie derivative to arbitrary tensor fields 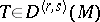 can be defined in the same way as the covariant derivative:
can be defined in the same way as the covariant derivative:
where 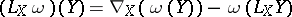 ,
, 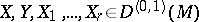 and
and 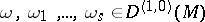 . This implies in local coordinates,
. This implies in local coordinates,
3) The exterior differential or exterior derivative is a linear operator 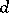 assigning to an (exterior) differential form
assigning to an (exterior) differential form 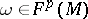 of degree
of degree 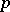 a differential form
a differential form 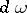 of degree
of degree 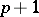 such that the following compatibility with the wedge product (exterior product) of differential forms is satisfied:
such that the following compatibility with the wedge product (exterior product) of differential forms is satisfied:
where 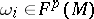 . Furthermore, one assumes that for a smooth function
. Furthermore, one assumes that for a smooth function 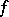 (a differential form of degree
(a differential form of degree  ),
), 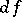 is given by the usual differential of
is given by the usual differential of 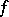 and that
and that 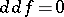 . This implies
. This implies 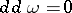 in general. For
in general. For 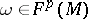 , the exterior differential can be described by:
, the exterior differential can be described by:
If in local coordinates 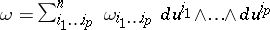 , then
, then
The fundamental operators of classical vector analysis may be described in terms of forms and exterior differentiation. For instance, the operator 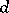 , acting on differential forms of degree
, acting on differential forms of degree  in
in 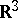 , corresponds to the operator
, corresponds to the operator 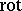 (
(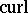 ). Differential forms are the suitable objects for the theory of integration on manifolds. Using the exterior derivative, the general form of the Stokes theorem can be given.
). Differential forms are the suitable objects for the theory of integration on manifolds. Using the exterior derivative, the general form of the Stokes theorem can be given.
4) As an example of the application of tensor analysis in differential geometry, the curvature tensor 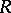 of a linear connection should be mentioned. This tensor is of type
of a linear connection should be mentioned. This tensor is of type 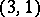 . In terms of the corresponding covariant derivative
. In terms of the corresponding covariant derivative  and vector fields
and vector fields 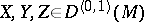 ,
, 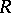 is given as follows:
is given as follows:
where, as usual, the contravariant entry is identified with a vector-valued multilinear mapping. In case of the Levi-Civita connection of a Riemannian metric 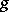 one obtains for the components
one obtains for the components 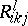 of
of 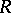 :
:
where the connection coefficients are obtained from the metric as follows:
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
| [a2] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
| [a3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963) |
How to Cite This Entry:
Tensor analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tensor_analysis&oldid=13841
This article was adapted from an original article by B. Wegner (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article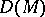 of differentiable tensor fields over a differentiable manifold
of differentiable tensor fields over a differentiable manifold  . Also the extension of this theory to more general geometric objects than tensor fields, such as tensor densities, vector-valued differential forms, etc. is considered as a part of tensor analysis.
. Also the extension of this theory to more general geometric objects than tensor fields, such as tensor densities, vector-valued differential forms, etc. is considered as a part of tensor analysis.
 is a linear mapping
is a linear mapping 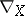 of the vector space
of the vector space 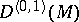 into itself satisfying the following conditions:
into itself satisfying the following conditions:

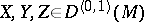 and
and 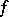 and
and 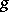 are smooth functions on
are smooth functions on 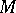 . In this interpretation the vector field
. In this interpretation the vector field 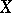 is considered as a derivation on functions, i.e. in local coordinates
is considered as a derivation on functions, i.e. in local coordinates 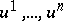 with
with 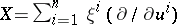 , for the derivative of the function
, for the derivative of the function 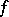 one has
one has 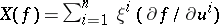 . The prescription of such an operator
. The prescription of such an operator 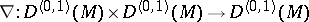 defines a linear connection and a parallel displacement along curves on
defines a linear connection and a parallel displacement along curves on 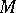 .
.
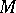 can be characterized by the properties that it is a derivation preserving the type of the tensor field and commuting with contraction. Regarding a tensor field of type
can be characterized by the properties that it is a derivation preserving the type of the tensor field and commuting with contraction. Regarding a tensor field of type 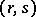 as a field of multilinear mappings which are defined on
as a field of multilinear mappings which are defined on  copies of the corresponding tangent space and
copies of the corresponding tangent space and  copies of the cotangent space, this extension is defined for
copies of the cotangent space, this extension is defined for 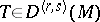 as follows:
as follows:
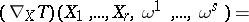
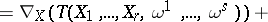
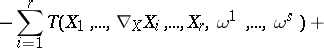
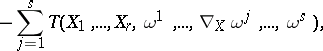
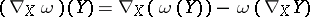 ,
,  and
and  . This implies in local coordinates, using the notations introduced above and the connection coefficients
. This implies in local coordinates, using the notations introduced above and the connection coefficients 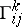 given by
given by 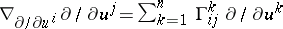 , the following formula in terms of the components
, the following formula in terms of the components 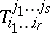 of
of 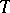 :
:
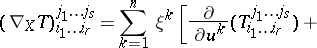
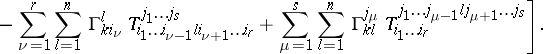
 of the tensor field
of the tensor field  by
by
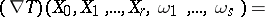
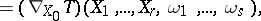
 presented above. In the case of the Levi-Civita connection of a Riemannian metric on
presented above. In the case of the Levi-Civita connection of a Riemannian metric on 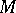 , the trace of the covariant differential of
, the trace of the covariant differential of 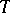 with respect to the first and some other covariant entry leads to an extension of the divergence to tensor fields.
with respect to the first and some other covariant entry leads to an extension of the divergence to tensor fields.
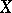 is the mapping
is the mapping 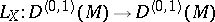 defined by
defined by 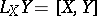 , where
, where 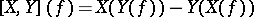 for any smooth function
for any smooth function 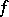 on
on 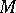 . The extension of the Lie derivative to arbitrary tensor fields
. The extension of the Lie derivative to arbitrary tensor fields 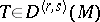 can be defined in the same way as the covariant derivative:
can be defined in the same way as the covariant derivative:
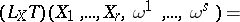
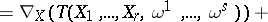
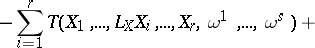
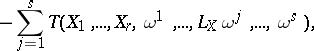
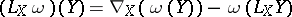 ,
, 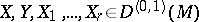 and
and 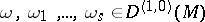 . This implies in local coordinates,
. This implies in local coordinates,
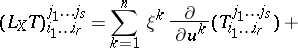
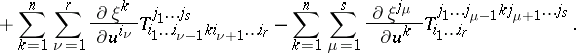
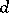 assigning to an (exterior) differential form
assigning to an (exterior) differential form 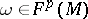 of degree
of degree 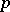 a differential form
a differential form 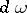 of degree
of degree 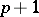 such that the following compatibility with the wedge product (exterior product) of differential forms is satisfied:
such that the following compatibility with the wedge product (exterior product) of differential forms is satisfied:
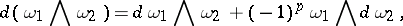
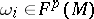 . Furthermore, one assumes that for a smooth function
. Furthermore, one assumes that for a smooth function 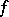 (a differential form of degree
(a differential form of degree  ),
), 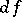 is given by the usual differential of
is given by the usual differential of 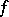 and that
and that 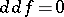 . This implies
. This implies 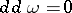 in general. For
in general. For 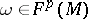 , the exterior differential can be described by:
, the exterior differential can be described by:
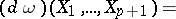
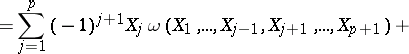
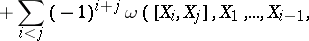
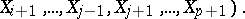
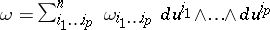 , then
, then
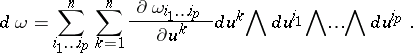
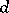 , acting on differential forms of degree
, acting on differential forms of degree  in
in 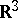 , corresponds to the operator
, corresponds to the operator 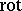 (
(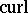 ). Differential forms are the suitable objects for the theory of integration on manifolds. Using the exterior derivative, the general form of the Stokes theorem can be given.
). Differential forms are the suitable objects for the theory of integration on manifolds. Using the exterior derivative, the general form of the Stokes theorem can be given.
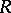 of a linear connection should be mentioned. This tensor is of type
of a linear connection should be mentioned. This tensor is of type 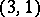 . In terms of the corresponding covariant derivative
. In terms of the corresponding covariant derivative  and vector fields
and vector fields 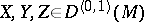 ,
, 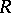 is given as follows:
is given as follows:
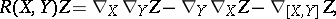
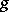 one obtains for the components
one obtains for the components 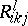 of
of 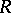 :
: