Teichmüller space
From Encyclopedia of Mathematics
A metric space 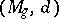 with as points abstract Riemann surfaces (that is, classes
with as points abstract Riemann surfaces (that is, classes 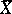 of conformally-equivalent Riemann surfaces
of conformally-equivalent Riemann surfaces  of genus
of genus 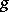 (cf. Riemann surfaces, conformal classes of) with singled out equivalent (with respect to the identity mapping) systems
(cf. Riemann surfaces, conformal classes of) with singled out equivalent (with respect to the identity mapping) systems 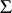 of generators of the fundamental group
of generators of the fundamental group 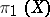 , and in which the distance
, and in which the distance 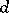 between
between 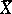 and
and 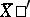 is equal to
is equal to 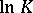 , where the constant
, where the constant 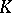 is the dilatation of the Teichmüller mapping (of the quasi-conformal mapping
is the dilatation of the Teichmüller mapping (of the quasi-conformal mapping 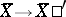 giving the smallest maximum dilatation among all such mappings). Introduced by O. Teichmüller [1].
giving the smallest maximum dilatation among all such mappings). Introduced by O. Teichmüller [1].
References
| [1] | O. Teichmüller, "Extremale quasikonforme Abbildungen und quadratische Differentialen" Abhandl. Preuss. Akad. Wissenschaft. Math.-Nat. Kl. , 22 (1939) pp. 3–197 |
| [2a] | L. Bers, "Quasi-conformal mappings and Teichmüller's theorem" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 89–119 |
| [2b] | L.V. Ahlfors, "The complex analytic structure of the space of Riemann surfaces" R. Nevanlinna (ed.) et al. (ed.) , Analytic functions , Princeton Univ. Press (1960) pp. 45–66 |
| [2c] | L. Bers, "Spaces of Riemann surfaces" , Proc. Intern. Congress Mathematicians, Edinburgh 1958 , Cambridge Univ. Press (1959) pp. 349–361 |
| [2d] | L. Bers, "Simultaneous uniformization" Bull. Amer. Math. Soc. , 66 (1960) pp. 94–97 |
| [2e] | L. Bers, "Holomorphic differentials as functions of moduli" Bull. Amer. Math. Soc. , 67 (1961) pp. 206–210 |
| [2f] | L. Ahlfors, "On quasiconformal mappings" J. d'Anal. Math. , 3 (1954) pp. 1–58; 207–208 |
| [3] | S.L. Krushkal, "Quasi-conformal mappings and Riemann surfaces" , Halsted (1979) (Translated from Russian) |
Comments
References
| [a1] | F.P. Gardiner, "Teichmüller theory and quadratic differentials" , Wiley (1987) |
| [a2] | O. Lehto, "Univalent functions and Teichmüller spaces" , Springer (1987) |
| [a3] | S. Nag, "The complex analytic theory of Teichmüller spaces" , Wiley (1988) |
How to Cite This Entry:
Teichmüller space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Teichm%C3%BCller_space&oldid=15836
Teichmüller space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Teichm%C3%BCller_space&oldid=15836
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article