Taylor series
A power series
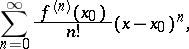 | (1) |
where the numerical function 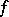 is defined in some neighbourhood of the point
is defined in some neighbourhood of the point 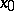 and has at this point derivatives of all orders. The partial sums of a Taylor series are Taylor polynomials (cf. Taylor polynomial).
and has at this point derivatives of all orders. The partial sums of a Taylor series are Taylor polynomials (cf. Taylor polynomial).
If 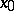 is a complex number and the function
is a complex number and the function 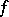 is defined in some neighbourhood of
is defined in some neighbourhood of 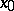 in the field of complex numbers and is differentiable at
in the field of complex numbers and is differentiable at 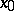 , then there exists a neighbourhood of
, then there exists a neighbourhood of 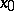 in which
in which 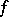 is the sum of its Taylor series (1) (see Power series). If, however,
is the sum of its Taylor series (1) (see Power series). If, however, 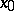 is a real number and the function
is a real number and the function 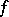 is defined in some neighbourhood of
is defined in some neighbourhood of 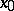 in the field of real numbers and has at
in the field of real numbers and has at 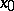 derivatives of all orders, then there may be no neighbourhood of
derivatives of all orders, then there may be no neighbourhood of 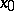 in which
in which 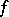 is the sum of its Taylor series. For instance, the function
is the sum of its Taylor series. For instance, the function
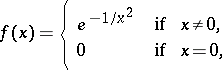 | (2) |
is differentiable infinitely many times on the entire real axis, is equal to 0 only at the point 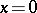 , but all coefficients of its Taylor series at this point are equal to 0.
, but all coefficients of its Taylor series at this point are equal to 0.
If a function is the sum in some neighbourhood of a given point of a power series with centre at that point, then such a series is unique and is the Taylor series of this function at the given point. However, one and the same power series can be the Taylor series of different real functions. Indeed, the power series all coefficients of which are equal to 0 is the Taylor series both of the function identically equal to 0 on the entire real axis and of the function (2) at the point 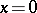 .
.
A sufficient condition for the convergence of the Taylor series (1) to the real-valued function 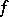 on an interval
on an interval 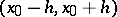 is the existence of a common bound for all its derivatives in this interval.
is the existence of a common bound for all its derivatives in this interval.
The Taylor series can be generalized to the case of mappings of subsets of linear normed spaces into similar spaces, and in particular to numerical functions of several variables and to functions of a matrix argument.
The series (1) was published by B. Taylor in 1715, a series reducible to the series (1) by a simple transformation was published by Johann I. Bernoulli in 1694.
References
| [1] | V.A. Il'in, V.A. Sadovnichii, B.Kh. Sendov, "Mathematical analysis" , Moscow (1979) (In Russian) |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
Comments
For references see also Taylor formula.
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) |
| [a2] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1960) (Translated from French) |
Taylor series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Taylor_series&oldid=15684