Difference between revisions of "Taylor joint spectrum"
(Importing text file) |
m (Automatically changed introduction) |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 192 formulas, 188 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $\Lambda \equiv \Lambda [ e ] \equiv \Lambda _ { n } [ e ]$ be the [[Exterior algebra|exterior algebra]] on $n$ generators $e _ { 1 } , \ldots , e _ { n }$, with identity $e _ { 0 } \equiv 1$. $\Lambda$ is the algebra of forms in $e _ { 1 } , \ldots , e _ { n }$ with complex coefficients, subject to the collapsing property $e _ { i } e _ { j } + e _ { j } e _ { i } = 0$ ($1 \leq i , j \leq n$). Let $E _ { i } : \Lambda \rightarrow \Lambda$ denote the creation operator, given by $E _ { i } \xi : = e _ { i } \xi$ ($\xi \in \Lambda$, $1 \leq i \leq n$). If one declares $\{ e _ { i_1 } , \ldots , e _ { i_k } , i , 1 \leq i _ { 1 } < \ldots < i _ { k } \leq n \}$ to be an orthonormal basis, the exterior algebra $\Lambda$ becomes a [[Hilbert space|Hilbert space]], admitting an orthogonal decomposition $\Lambda = \oplus _ { k = 1 } ^ { n } \Lambda ^ { k }$, where $\operatorname { dim } \Lambda ^ { k } = \left( \begin{array} { l } { n } \\ { k } \end{array} \right)$. Thus, each $\xi \in \Lambda$ admits a unique orthogonal decomposition $\xi = e _ { i } \xi ^ { \prime } + \xi ^ { \prime \prime }$, where $\xi ^ { \prime }$ and $\xi ''$ have no $e _ { i }$ contribution. It then readily follows that $E _ { i } ^ { * } \xi = \xi ^ { \prime }$. Indeed, each $E_i$ is a partial isometry, satisfying $E _ { i } ^ { * } E _ { j } + E _ { j } E _ { i } ^ { * } = \delta _ { i j }$ ($1 \leq i , j \leq n$). | ||
| − | + | Let $\mathcal{X}$ be a [[Normed space|normed space]], let $A \equiv ( A _ { 1 } , \dots , A _ { n } )$ be a commuting $n$-tuple of bounded operators on $\mathcal{X}$ and set $\Lambda ( {\cal X} ) : = {\cal X} \otimes _ { {\bf C} } \Lambda$. One defines $D _ { A } : \Lambda ( \mathcal{X} ) \rightarrow \Lambda ( \mathcal{X} )$ by $D _ { A } : = \sum _ { i = 1 } ^ { n } A _ { i } \otimes E _ { i }$. Clearly, $D _ { A } ^ { 2 } = 0$, so <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005034.png"/>. | |
| − | The | + | The commuting $n$-tuple $A$ is said to be non-singular on $\mathcal{X}$ if $\operatorname { Ran } D _ { A } = \operatorname { Ker } D_ { A } $. The Taylor joint spectrum, or simply the Taylor spectrum, of $A$ on $\mathcal{X}$ is the set |
| − | + | \begin{equation*} \sigma _ { \text{T} } ( A , {\cal X} ) : = \{ \lambda \in {\bf C} ^ { n } : A - \lambda \text { is singular } \}. \end{equation*} | |
| − | + | The decomposition $\Lambda = \oplus _ { k = 1 } ^ { n } \Lambda ^ { k }$ gives rise to a cochain complex $K ( A , \mathcal{X} )$, the so-called [[Koszul complex|Koszul complex]] associated to $A$ on $\mathcal{X}$, as follows: | |
| − | + | \begin{equation*} K ( A , {\cal X} ) : 0 \rightarrow \Lambda ^ { 0 } ( {\cal X} ) \stackrel { D _ { A } ^ { 0 } } { \rightarrow } \ldots \stackrel { D _ { A } ^ { n - 1 } } { \rightarrow } \Lambda ^ { n } ( {\cal X} ) \rightarrow 0, \end{equation*} | |
| − | + | where $D _ { A } ^ { k }$ denotes the restriction of $D _ { A }$ to the subspace $\Lambda ^ { k } ( \mathcal{X} )$. Thus, | |
| − | + | \begin{equation*} \sigma _ { \operatorname{T} } ( A , {\cal X} ) = \{ \lambda \in \mathbf{C} ^ { n } : K ( A - \lambda , {\cal X} ) \text{ is not exact}\}. \end{equation*} | |
| − | |||
| − | + | J.L. Taylor showed in [[#References|[a17]]] that if $\mathcal{X}$ is a [[Banach space|Banach space]], then $\sigma _ { \text{T} } ( A , \mathcal X )$ is compact, non-empty, and contained in $\sigma ^ { \prime } ( A )$, the (joint) algebraic spectrum of $A$ (cf. also [[Spectrum of an operator|Spectrum of an operator]]) with respect to the commutant of $A$, $( A ) ^ { \prime } : = \{ B \in \mathcal{L} ( \mathcal{X} ) : B A = A B \}$. Moreover, $\sigma _{\operatorname{T}}$ carries an analytic [[Functional calculus|functional calculus]] with values in the double commutant of $A$, so that, in particular, $\sigma _{\operatorname{T}}$ possesses the projection property. | |
| − | + | ===Example: $n = 1$.=== | |
| + | For $n = 1$, $D _ { A }$ admits the following $( 2 \times 2 )$-matrix relative to the direct sum decomposition $( \mathcal{X} \otimes e _ { 0 } ) \oplus ( \mathcal{X} \otimes e_ { 1 } )$: | ||
| − | = | + | \begin{equation*} D _ { A } = \left( \begin{array} { l l } { 0 } & { 0 } \\ { A } & { 0 } \end{array} \right). \end{equation*} |
| − | |||
| − | + | Then $\operatorname { Ker } D _ { A } / \operatorname { Ran } D _ { A } = \operatorname { Ker } A \oplus ({\cal X} / \operatorname { Ran } A )$. It follows at once that $\sigma _{\operatorname{T}}$ agrees with $\sigma$, the spectrum of $A$. | |
| − | + | ===Example: $n = 2$.=== | |
| + | For $n = 2$, | ||
| − | + | \begin{equation*} D _ { A } = \left( \begin{array} { c c c c } { 0 } & { 0 } & { 0 } & { 0 } \\ { A _ { 1 } } & { 0 } & { 0 } & { 0 } \\ { A _ { 2 } } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - A _ { 2 } } & { A _ { 1 } } & { 0 } \end{array} \right), \end{equation*} | |
| + | |||
| + | so <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t13005073.png"/>. | ||
| + | |||
| + | Note that since $\sigma _{\operatorname{T}}$ is defined in terms of the actions of the operators $A_i$ on vectors of $\mathcal{X}$, it is intrinsically "spatial" , as opposed to $\sigma ^ { \prime }$, $\sigma ^ { \prime \prime }$ and other algebraic joint spectra. $\sigma _{\operatorname{T}}$ contains other well-known spatial spectra, like $\sigma _ { \text{p} }$ (the point spectrum), $\sigma _ { \pi }$ (the approximate point spectrum) and $\sigma _ { \delta }$ (the defect spectrum). Moreover, if $\mathcal{B}$ is a commutative Banach algebra, $a \equiv ( a _ { 1 } , \dots , a _ { n } )$, with each $a _ { i } \in \mathcal{B}$, and $L _ { a }$ denotes the $n$-tuple of left multiplications by the $a_i$s, it is not hard to show that $\sigma _ { \text{T} } ( L _ { a } , \mathcal{B} ) = \sigma _ { \mathcal{B} } ( a )$. As a matter of fact, the same result holds when $\mathcal{B}$ is not commutative, provided all the $a_i$s come from the centre of $\mathcal{B}$. | ||
===Spectral permanence.=== | ===Spectral permanence.=== | ||
| − | When | + | When $\mathcal{B}$ is a $C ^ { * }$-algebra, say $\mathcal{B} \subseteq \mathcal{L} ( \mathcal{H} )$, then $\sigma _ { T } ( L _ { a } , \mathcal{B} ) = \sigma _ { T } ( a , \mathcal{H} )$ [[#References|[a9]]]. This fact, known as spectral permanence for the Taylor spectrum, shows that for $C ^ { * }$-algebra elements (and also for Hilbert space operators), the non-singularity of $L _ { a }$ is equivalent to the invertibility of the associated Dirac operator $D _ { a } + D _ { a^{*} } ^ { t }$. |
===Finite-dimensional case.=== | ===Finite-dimensional case.=== | ||
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050100.png" />, | + | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050100.png"/>, |
| − | + | \begin{equation*} \sigma _ { \text{p} } = \sigma _ { \text{l} } = \sigma _ { \pi } = \sigma _ { \delta } = \sigma _ { \text{r} } = \sigma _ { \text{T} } = \sigma ^ { \prime } = \sigma ^ { \prime \prime } = \widehat { \sigma }, \end{equation*} | |
| − | where | + | where $\sigma_{\text{l}}$, $\sigma _ { \text{r} }$ and $\hat { \sigma }$ denote the left, right and polynomially convex spectra, respectively. As a matter of fact, in this case the commuting $n$-tuple $A$ can be simultaneously triangularized as $A _ { k } \equiv ( a _ { i ,\, j } ^ { ( k ) } ) _ { i ,\, j = 1 } ^ { \operatorname { dim } \mathcal{X} }$, and |
| − | + | \begin{equation*} \sigma _ { T } ( A , \mathcal{X} ) = \left\{ ( a _ {ii} ^ { ( 1 ) } , \ldots , a _ { ii } ^ { ( n ) } ) : 1 \leq i \leq \operatorname { dim } \mathcal{X} \right\}. \end{equation*} | |
===Case of compact operators.=== | ===Case of compact operators.=== | ||
| − | If | + | If $A$ is a commuting $n$-tuple of compact operators acting on a Banach space $\mathcal{X}$, then $\sigma _ { \text{T} } ( A , \mathcal X )$ is countable, with $( 0 , \ldots , 0 )$ as the only accumulation point. Moreover, $\sigma _ { \pi } ( A , \mathcal{X} ) = \sigma _ { \delta } ( A , \mathcal{X} ) = \sigma _ { \text{T} } ( A , \mathcal{X} )$. |
===Invariant subspaces.=== | ===Invariant subspaces.=== | ||
| − | If | + | If $\mathcal{X}$ is a Banach space, $\mathcal{Y}$ is a closed subspace of $\mathcal{X}$ and $A$ is a commuting $n$-tuple leaving $\mathcal{Y}$ invariant, then the union of any two of the sets $\sigma _ { \text{T} } ( A , \mathcal X )$, $\sigma _ { \text{T} } ( A , \mathcal{Y} )$ and $\sigma _ { T } ( A , \mathcal{X} / \mathcal{Y} )$ contains the third [[#References|[a17]]]. This can be seen by looking at the long cohomology sequence associated to the Koszul complex and the canonical short exact sequence $0 \rightarrow {\cal Y \rightarrow X \rightarrow X / Y }\rightarrow 0$. |
===Additional properties.=== | ===Additional properties.=== | ||
| − | In addition to the above-mentioned properties of | + | In addition to the above-mentioned properties of $\sigma _{\operatorname{T}}$, the following facts can be found in the survey article [[#References|[a10]]] and the references therein: |
| − | i) | + | i) $\sigma _{\operatorname{T}}$ gives rise to a compact non-empty subset $M _ { \sigma _ { \operatorname{T} } } (\cal B , X )$ of the maximal ideal space of any commutative Banach algebra $\mathcal{B}$ containing $A$, in such a way that $\sigma _ { \text{T} } ( A , \mathcal{X} ) = \hat { A } ( M _ { \sigma _ { \text{T} } } ( \mathcal{B} , \mathcal{X} ) )$ [[#References|[a17]]]; |
| − | ii) for | + | ii) for $n = 2$, $\partial \sigma _ { T } ( A , \mathcal{H} ) \subseteq \partial \sigma _ { H } ( A , \mathcal{H} )$, where $\sigma _ { \text{H} } : = \sigma _ { \text{I} } \cup \sigma _ { \text{r} }$ denotes the Harte spectrum; |
iii) the upper semi-continuity of separate parts holds for the Taylor spectrum; | iii) the upper semi-continuity of separate parts holds for the Taylor spectrum; | ||
| − | iv) every isolated point in | + | iv) every isolated point in $\sigma _ { \mathcal{B} } ( A )$ is an isolated point of $\sigma _ { \text{T} } ( A , \mathcal{H} )$ (and, a fortiori, an isolated point of $\sigma _ { \text{l} } ( A , \mathcal{H} ) \cap \sigma _ { \text{r} } ( A , \mathcal{H} )$); |
| − | v) if | + | v) if $0 \in \sigma _ { \text{T} } ( A , \mathcal{H} )$, up to approximate unitary equivalence one can always assume that $\overline { \operatorname { Ran } D _ { A } } \neq \operatorname { Ker } D _ { A }$ [[#References|[a5]]]; |
| − | vi) the functional calculus introduced by Taylor in [[#References|[a18]]] admits a concrete realization in terms of the Bochner–Martinelli kernel (cf. [[Bochner–Martinelli representation formula|Bochner–Martinelli representation formula]]) in case | + | vi) the functional calculus introduced by Taylor in [[#References|[a18]]] admits a concrete realization in terms of the Bochner–Martinelli kernel (cf. [[Bochner–Martinelli representation formula|Bochner–Martinelli representation formula]]) in case $A$ acts on a Hilbert space or on a [[C*-algebra|$C ^ { * }$-algebra]] [[#References|[a20]]]; |
vii) M. Putinar established in [[#References|[a13]]] the uniqueness of the functional calculus, provided it extends the polynomial calculus. | vii) M. Putinar established in [[#References|[a13]]] the uniqueness of the functional calculus, provided it extends the polynomial calculus. | ||
| − | ===Fredholm | + | ===Fredholm $n$-tuples.=== |
| − | In a way entirely similar to the development of Fredholm theory, one can define the notion of Fredholm | + | In a way entirely similar to the development of Fredholm theory, one can define the notion of Fredholm $n$-tuple: a commuting $n$-tuple $A$ is said to be Fredholm on $\mathcal{X}$ if the associated Koszul complex $K ( A , \mathcal{X} )$ has finite-dimensional cohomology spaces. The Taylor essential spectrum of $A$ on $\mathcal{X}$ is then |
| − | + | \begin{equation*} \sigma _ { \text{Te} } ( A , \mathcal{X} ) : = \{ \lambda \in \mathbf{C} ^ { n } : A - \lambda \ \text{is not Fredholm} \}. \end{equation*} | |
| − | The Fredholm index of | + | The Fredholm index of $A$ is defined as the [[Euler characteristic|Euler characteristic]] of $K ( A , \mathcal{X} )$. For example, if $n = 2$, $\operatorname{index}( A ) = \operatorname { dim } \operatorname { Ker } D _ { A } ^ { 0 } - \operatorname { dim } ( \operatorname { Ker } D _ { A } ^ { 1 } / \operatorname { Ran } D _ { A } ^ { 0 } ) + \operatorname { dim } ( {\cal X} / \operatorname { Ran } D _ { A } ^ { 1 } )$. In a Hilbert space, $\sigma _ { \text{Te} } ( A , \mathcal{H} ) = \sigma _ { \text{T} } ( L _ { a } , \mathcal{Q} ( \mathcal{H} ) )$, where $a : = \pi ( A )$ is the coset of $A$ in the Calkin algebra for $\mathcal{H}$. |
===Example.=== | ===Example.=== | ||
| − | If | + | If $\mathcal H = H ^ { 2 } ( S ^ { 3 } )$ and $A _ { i } : = M _ { z _ { i } }$ ($i = 1,2$), then $\sigma _ { \text{l}} ( A ) = \sigma _ { \text{le} } ( A ) = \sigma _ { \text{re} } ( A ) = \sigma _ { \text{Te} } ( A ) = S ^ { 3 }$, $\sigma _ { r } ( A ) = \sigma _ { T } ( A ) = \mathbf{B} _ { 4 }$, and $\operatorname{index}( A - \lambda ) = 1$ ($\lambda \in \mathbf{B} _ { 4 }$). |
| − | The Taylor spectral and Fredholm theories of multiplication operators acting on Bergman spaces over Reinhardt domains or bounded pseudo-convex domains, or acting on the Hardy spaces over the Shilov boundary of bounded symmetric domains on several complex variables, have been described in [[#References|[a4]]], [[#References|[a3]]], [[#References|[a6]]], [[#References|[a7]]], [[#References|[a8]]], [[#References|[a16]]], [[#References|[a15]]], [[#References|[a19]]], and [[#References|[a21]]]; for Toeplitz operators with | + | The Taylor spectral and Fredholm theories of multiplication operators acting on Bergman spaces over Reinhardt domains or bounded pseudo-convex domains, or acting on the Hardy spaces over the [[Shilov boundary]] of bounded symmetric domains on several complex variables, have been described in [[#References|[a4]]], [[#References|[a3]]], [[#References|[a6]]], [[#References|[a7]]], [[#References|[a8]]], [[#References|[a16]]], [[#References|[a15]]], [[#References|[a19]]], and [[#References|[a21]]]; for Toeplitz operators with $H ^ { \infty }$ symbols acting on bounded pseudo-convex domains, concrete descriptions appear in [[#References|[a11]]]. |
===Spectral inclusion.=== | ===Spectral inclusion.=== | ||
| − | If | + | If $S$ is a subnormal $n$-tuple acting on $\mathcal{H}$ with minimal normal extension $N$ acting on $\mathcal{K}$ (cf. also [[Normal operator|Normal operator]]), $\sigma _ { \text{T} } ( N , \mathcal{K} ) \subseteq \sigma _ { \text{T} } ( S , \mathcal{H} ) \subseteq \hat { \sigma } ( N , \mathcal{K} )$ [[#References|[a14]]]. |
===Left and right multiplications.=== | ===Left and right multiplications.=== | ||
| − | For | + | For $A$ and $B$ two commuting $n$-tuples of operators on a Hilbert space $\mathcal{H}$, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130050/t130050177.png"/> and $R _ { B }$ the associated $n$-tuples of left and right multiplication operators [[#References|[a5]]], |
| − | + | \begin{equation*} \sigma _ { \operatorname{T} } ( ( L _ { A } , R _ { B } ) , \mathcal{L} ( \mathcal{H} ) ) = \sigma _ { \operatorname{T} } ( A , \mathcal{H} ) \times \sigma _ { T } ( B , \mathcal{H} ) \end{equation*} | |
and | and | ||
| − | + | \begin{equation*} \sigma _ { \text{Te} } ( ( L _ { A } , R _ { B } ) , \mathcal{L} ( \mathcal{H} ) ) = \end{equation*} | |
| − | + | \begin{equation*} = [ \sigma _ { \operatorname{Te} } ( A , {\cal H} ) \times \sigma _ { \operatorname{T} } ( B , {\cal H} ) ] \bigcup [ \sigma _ { \operatorname{T} } ( A , {\cal H} ) \times \sigma _ { \operatorname{Te} } ( B , {\cal H} ) ]. \end{equation*} | |
| − | During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [[#References|[a2]]], [[#References|[a11]]], [[#References|[a20]]], [[#References|[a10]]], [[#References|[a1]]]. There is also a parallel | + | During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [[#References|[a2]]], [[#References|[a11]]], [[#References|[a20]]], [[#References|[a10]]], [[#References|[a1]]]. There is also a parallel "local spectral theory" , described in [[#References|[a11]]], [[#References|[a12]]] and [[#References|[a20]]]. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E. Albrecht, F.-H. Vasilescu, "Semi-Fredholm complexes" ''Oper. Th. Adv. Appl.'' , '''11''' (1983) pp. 15–39 {{MR|0789629}} {{ZBL|0527.47008}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C.-G. Ambrozie, F.-H. Vasilescu, "Banach space complexes" , Kluwer Acad. Publ. (1995) {{MR|1357165}} {{ZBL|0837.47009}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> C. Berger, L. Coburn, A. Koranyi, "Opérateurs de Wiener–Hopf sur les spheres de Lie" ''C.R. Acad. Sci. Paris Sér. A'' , '''290''' (1980) pp. 989–991 {{MR|584284}} {{ZBL|0436.47021}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Berger, L. Coburn, "Wiener–Hopf operators on $U _ { 2 }$" ''Integral Eq. Oper. Th.'' , '''2''' (1979) pp. 139–173 {{MR|0543881}} {{ZBL|0434.47019}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> R. Curto, L. Fialkow, "The spectral picture of $( L_{A} , R _ { B } )$" ''J. Funct. Anal.'' , '''71''' (1987) pp. 371–392 {{MR|0880986}} {{ZBL|0626.47018}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Curto, P. Muhly, "$C ^ { * }$-algebras of multiplication operators on Bergman spaces" ''J. Funct. Anal.'' , '''64''' (1985) pp. 315–329 {{MR|0813203}} {{ZBL|0583.46049}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> R. Curto, N. Salinas, "Spectral properties of cyclic subnormal $m$-tuples" ''Amer. J. Math.'' , '''107''' (1985) pp. 113–138 {{MR|778091}} {{ZBL|}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> R. Curto, K. Yan, "The spectral picture of Reinhardt measures" ''J. Funct. Anal.'' , '''131''' (1995) pp. 279–301 {{MR|1345033}} {{ZBL|0826.47002}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> R. Curto, "Spectral permanence for joint spectra" ''Trans. Amer. Math. Soc.'' , '''270''' (1982) pp. 659–665 {{MR|0645336}} {{ZBL|0508.47039}} {{ZBL|0491.47020}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> R. Curto, "Applications of several complex variables to multiparameter spectral theory" J.B. Conway (ed.) B.B. Morrel (ed.) , ''Surveys of Some Recent Results in Operator Theory II'' , ''Pitman Res. Notes in Math.'' , '''192''' , Longman Sci. Tech. (1988) pp. 25–90 {{MR|0976843}} {{ZBL|0827.47005}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> J. Eschmeier, M. Putinar, "Spectral decompositions and analytic sheaves" , ''London Math. Soc. Monographs'' , Oxford Sci. Publ. (1996) {{MR|1420618}} {{ZBL|0855.47013}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> K. Laursen, M. Neumann, "Introduction to local spectral theory" , ''London Math. Soc. Monographs'' , Oxford Univ. Press (2000) {{MR|1747914}} {{ZBL|0957.47004}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> M. Putinar, "Uniqueness of Taylor's functional calculus" ''Proc. Amer. Math. Soc.'' , '''89''' (1983) pp. 647–650 {{MR|718990}} {{ZBL|}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> M. Putinar, "Spectral inclusion for subnormal $n$-tuples" ''Proc. Amer. Math. Soc.'' , '''90''' (1984) pp. 405–406 {{MR|728357}} {{ZBL|}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> N. Salinas, A. Sheu, H. Upmeier, "Toeplitz operators on pseudoconvex domains and foliation $C ^ { * }$-algebras" ''Ann. of Math.'' , '''130''' (1989) pp. 531–565 {{MR|1025166}} {{ZBL|}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> N. Salinas, "The $\overline { \partial }$-formalism and the $C ^ { * }$-algebra of the Bergman $n$-tuple" ''J. Oper. Th.'' , '''22''' (1989) pp. 325–343 {{MR|1043731}} {{ZBL|}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> J.L. Taylor, "A joint spectrum for several commuting operators" ''J. Funct. Anal.'' , '''6''' (1970) pp. 172–191 {{MR|0268706}} {{ZBL|0233.47024}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> J.L. Taylor, "The analytic functional calculus for several commuting operators" ''Acta Math.'' , '''125''' (1970) pp. 1–48 {{MR|0271741}} {{ZBL|0233.47025}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> H. Upmeier, "Toeplitz $C ^ { * }$-algebras on bounded symmetric domains" ''Ann. of Math.'' , '''119''' (1984) pp. 549–576 {{MR|744863}} {{ZBL|}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> F.-H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) {{MR|0690957}} {{ZBL|0495.47013}} </td></tr><tr><td valign="top">[a21]</td> <td valign="top"> U. Venugopalkrishna, "Fredholm operators associated with strongly pseudoconvex domains in $\mathbf{C} ^ { n }$" ''J. Funct. Anal.'' , '''9''' (1972) pp. 349–373 {{MR|0315502}} {{ZBL|0241.47023}} </td></tr></table> |
Latest revision as of 17:44, 1 July 2020
Let $\Lambda \equiv \Lambda [ e ] \equiv \Lambda _ { n } [ e ]$ be the exterior algebra on $n$ generators $e _ { 1 } , \ldots , e _ { n }$, with identity $e _ { 0 } \equiv 1$. $\Lambda$ is the algebra of forms in $e _ { 1 } , \ldots , e _ { n }$ with complex coefficients, subject to the collapsing property $e _ { i } e _ { j } + e _ { j } e _ { i } = 0$ ($1 \leq i , j \leq n$). Let $E _ { i } : \Lambda \rightarrow \Lambda$ denote the creation operator, given by $E _ { i } \xi : = e _ { i } \xi$ ($\xi \in \Lambda$, $1 \leq i \leq n$). If one declares $\{ e _ { i_1 } , \ldots , e _ { i_k } , i , 1 \leq i _ { 1 } < \ldots < i _ { k } \leq n \}$ to be an orthonormal basis, the exterior algebra $\Lambda$ becomes a Hilbert space, admitting an orthogonal decomposition $\Lambda = \oplus _ { k = 1 } ^ { n } \Lambda ^ { k }$, where $\operatorname { dim } \Lambda ^ { k } = \left( \begin{array} { l } { n } \\ { k } \end{array} \right)$. Thus, each $\xi \in \Lambda$ admits a unique orthogonal decomposition $\xi = e _ { i } \xi ^ { \prime } + \xi ^ { \prime \prime }$, where $\xi ^ { \prime }$ and $\xi ''$ have no $e _ { i }$ contribution. It then readily follows that $E _ { i } ^ { * } \xi = \xi ^ { \prime }$. Indeed, each $E_i$ is a partial isometry, satisfying $E _ { i } ^ { * } E _ { j } + E _ { j } E _ { i } ^ { * } = \delta _ { i j }$ ($1 \leq i , j \leq n$).
Let $\mathcal{X}$ be a normed space, let $A \equiv ( A _ { 1 } , \dots , A _ { n } )$ be a commuting $n$-tuple of bounded operators on $\mathcal{X}$ and set $\Lambda ( {\cal X} ) : = {\cal X} \otimes _ { {\bf C} } \Lambda$. One defines $D _ { A } : \Lambda ( \mathcal{X} ) \rightarrow \Lambda ( \mathcal{X} )$ by $D _ { A } : = \sum _ { i = 1 } ^ { n } A _ { i } \otimes E _ { i }$. Clearly, $D _ { A } ^ { 2 } = 0$, so 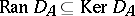 .
.
The commuting $n$-tuple $A$ is said to be non-singular on $\mathcal{X}$ if $\operatorname { Ran } D _ { A } = \operatorname { Ker } D_ { A } $. The Taylor joint spectrum, or simply the Taylor spectrum, of $A$ on $\mathcal{X}$ is the set
\begin{equation*} \sigma _ { \text{T} } ( A , {\cal X} ) : = \{ \lambda \in {\bf C} ^ { n } : A - \lambda \text { is singular } \}. \end{equation*}
The decomposition $\Lambda = \oplus _ { k = 1 } ^ { n } \Lambda ^ { k }$ gives rise to a cochain complex $K ( A , \mathcal{X} )$, the so-called Koszul complex associated to $A$ on $\mathcal{X}$, as follows:
\begin{equation*} K ( A , {\cal X} ) : 0 \rightarrow \Lambda ^ { 0 } ( {\cal X} ) \stackrel { D _ { A } ^ { 0 } } { \rightarrow } \ldots \stackrel { D _ { A } ^ { n - 1 } } { \rightarrow } \Lambda ^ { n } ( {\cal X} ) \rightarrow 0, \end{equation*}
where $D _ { A } ^ { k }$ denotes the restriction of $D _ { A }$ to the subspace $\Lambda ^ { k } ( \mathcal{X} )$. Thus,
\begin{equation*} \sigma _ { \operatorname{T} } ( A , {\cal X} ) = \{ \lambda \in \mathbf{C} ^ { n } : K ( A - \lambda , {\cal X} ) \text{ is not exact}\}. \end{equation*}
J.L. Taylor showed in [a17] that if $\mathcal{X}$ is a Banach space, then $\sigma _ { \text{T} } ( A , \mathcal X )$ is compact, non-empty, and contained in $\sigma ^ { \prime } ( A )$, the (joint) algebraic spectrum of $A$ (cf. also Spectrum of an operator) with respect to the commutant of $A$, $( A ) ^ { \prime } : = \{ B \in \mathcal{L} ( \mathcal{X} ) : B A = A B \}$. Moreover, $\sigma _{\operatorname{T}}$ carries an analytic functional calculus with values in the double commutant of $A$, so that, in particular, $\sigma _{\operatorname{T}}$ possesses the projection property.
Example: $n = 1$.
For $n = 1$, $D _ { A }$ admits the following $( 2 \times 2 )$-matrix relative to the direct sum decomposition $( \mathcal{X} \otimes e _ { 0 } ) \oplus ( \mathcal{X} \otimes e_ { 1 } )$:
\begin{equation*} D _ { A } = \left( \begin{array} { l l } { 0 } & { 0 } \\ { A } & { 0 } \end{array} \right). \end{equation*}
Then $\operatorname { Ker } D _ { A } / \operatorname { Ran } D _ { A } = \operatorname { Ker } A \oplus ({\cal X} / \operatorname { Ran } A )$. It follows at once that $\sigma _{\operatorname{T}}$ agrees with $\sigma$, the spectrum of $A$.
Example: $n = 2$.
For $n = 2$,
\begin{equation*} D _ { A } = \left( \begin{array} { c c c c } { 0 } & { 0 } & { 0 } & { 0 } \\ { A _ { 1 } } & { 0 } & { 0 } & { 0 } \\ { A _ { 2 } } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - A _ { 2 } } & { A _ { 1 } } & { 0 } \end{array} \right), \end{equation*}
so 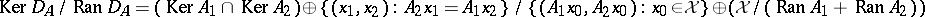 .
.
Note that since $\sigma _{\operatorname{T}}$ is defined in terms of the actions of the operators $A_i$ on vectors of $\mathcal{X}$, it is intrinsically "spatial" , as opposed to $\sigma ^ { \prime }$, $\sigma ^ { \prime \prime }$ and other algebraic joint spectra. $\sigma _{\operatorname{T}}$ contains other well-known spatial spectra, like $\sigma _ { \text{p} }$ (the point spectrum), $\sigma _ { \pi }$ (the approximate point spectrum) and $\sigma _ { \delta }$ (the defect spectrum). Moreover, if $\mathcal{B}$ is a commutative Banach algebra, $a \equiv ( a _ { 1 } , \dots , a _ { n } )$, with each $a _ { i } \in \mathcal{B}$, and $L _ { a }$ denotes the $n$-tuple of left multiplications by the $a_i$s, it is not hard to show that $\sigma _ { \text{T} } ( L _ { a } , \mathcal{B} ) = \sigma _ { \mathcal{B} } ( a )$. As a matter of fact, the same result holds when $\mathcal{B}$ is not commutative, provided all the $a_i$s come from the centre of $\mathcal{B}$.
Spectral permanence.
When $\mathcal{B}$ is a $C ^ { * }$-algebra, say $\mathcal{B} \subseteq \mathcal{L} ( \mathcal{H} )$, then $\sigma _ { T } ( L _ { a } , \mathcal{B} ) = \sigma _ { T } ( a , \mathcal{H} )$ [a9]. This fact, known as spectral permanence for the Taylor spectrum, shows that for $C ^ { * }$-algebra elements (and also for Hilbert space operators), the non-singularity of $L _ { a }$ is equivalent to the invertibility of the associated Dirac operator $D _ { a } + D _ { a^{*} } ^ { t }$.
Finite-dimensional case.
When 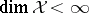 ,
,
\begin{equation*} \sigma _ { \text{p} } = \sigma _ { \text{l} } = \sigma _ { \pi } = \sigma _ { \delta } = \sigma _ { \text{r} } = \sigma _ { \text{T} } = \sigma ^ { \prime } = \sigma ^ { \prime \prime } = \widehat { \sigma }, \end{equation*}
where $\sigma_{\text{l}}$, $\sigma _ { \text{r} }$ and $\hat { \sigma }$ denote the left, right and polynomially convex spectra, respectively. As a matter of fact, in this case the commuting $n$-tuple $A$ can be simultaneously triangularized as $A _ { k } \equiv ( a _ { i ,\, j } ^ { ( k ) } ) _ { i ,\, j = 1 } ^ { \operatorname { dim } \mathcal{X} }$, and
\begin{equation*} \sigma _ { T } ( A , \mathcal{X} ) = \left\{ ( a _ {ii} ^ { ( 1 ) } , \ldots , a _ { ii } ^ { ( n ) } ) : 1 \leq i \leq \operatorname { dim } \mathcal{X} \right\}. \end{equation*}
Case of compact operators.
If $A$ is a commuting $n$-tuple of compact operators acting on a Banach space $\mathcal{X}$, then $\sigma _ { \text{T} } ( A , \mathcal X )$ is countable, with $( 0 , \ldots , 0 )$ as the only accumulation point. Moreover, $\sigma _ { \pi } ( A , \mathcal{X} ) = \sigma _ { \delta } ( A , \mathcal{X} ) = \sigma _ { \text{T} } ( A , \mathcal{X} )$.
Invariant subspaces.
If $\mathcal{X}$ is a Banach space, $\mathcal{Y}$ is a closed subspace of $\mathcal{X}$ and $A$ is a commuting $n$-tuple leaving $\mathcal{Y}$ invariant, then the union of any two of the sets $\sigma _ { \text{T} } ( A , \mathcal X )$, $\sigma _ { \text{T} } ( A , \mathcal{Y} )$ and $\sigma _ { T } ( A , \mathcal{X} / \mathcal{Y} )$ contains the third [a17]. This can be seen by looking at the long cohomology sequence associated to the Koszul complex and the canonical short exact sequence $0 \rightarrow {\cal Y \rightarrow X \rightarrow X / Y }\rightarrow 0$.
Additional properties.
In addition to the above-mentioned properties of $\sigma _{\operatorname{T}}$, the following facts can be found in the survey article [a10] and the references therein:
i) $\sigma _{\operatorname{T}}$ gives rise to a compact non-empty subset $M _ { \sigma _ { \operatorname{T} } } (\cal B , X )$ of the maximal ideal space of any commutative Banach algebra $\mathcal{B}$ containing $A$, in such a way that $\sigma _ { \text{T} } ( A , \mathcal{X} ) = \hat { A } ( M _ { \sigma _ { \text{T} } } ( \mathcal{B} , \mathcal{X} ) )$ [a17];
ii) for $n = 2$, $\partial \sigma _ { T } ( A , \mathcal{H} ) \subseteq \partial \sigma _ { H } ( A , \mathcal{H} )$, where $\sigma _ { \text{H} } : = \sigma _ { \text{I} } \cup \sigma _ { \text{r} }$ denotes the Harte spectrum;
iii) the upper semi-continuity of separate parts holds for the Taylor spectrum;
iv) every isolated point in $\sigma _ { \mathcal{B} } ( A )$ is an isolated point of $\sigma _ { \text{T} } ( A , \mathcal{H} )$ (and, a fortiori, an isolated point of $\sigma _ { \text{l} } ( A , \mathcal{H} ) \cap \sigma _ { \text{r} } ( A , \mathcal{H} )$);
v) if $0 \in \sigma _ { \text{T} } ( A , \mathcal{H} )$, up to approximate unitary equivalence one can always assume that $\overline { \operatorname { Ran } D _ { A } } \neq \operatorname { Ker } D _ { A }$ [a5];
vi) the functional calculus introduced by Taylor in [a18] admits a concrete realization in terms of the Bochner–Martinelli kernel (cf. Bochner–Martinelli representation formula) in case $A$ acts on a Hilbert space or on a $C ^ { * }$-algebra [a20];
vii) M. Putinar established in [a13] the uniqueness of the functional calculus, provided it extends the polynomial calculus.
Fredholm $n$-tuples.
In a way entirely similar to the development of Fredholm theory, one can define the notion of Fredholm $n$-tuple: a commuting $n$-tuple $A$ is said to be Fredholm on $\mathcal{X}$ if the associated Koszul complex $K ( A , \mathcal{X} )$ has finite-dimensional cohomology spaces. The Taylor essential spectrum of $A$ on $\mathcal{X}$ is then
\begin{equation*} \sigma _ { \text{Te} } ( A , \mathcal{X} ) : = \{ \lambda \in \mathbf{C} ^ { n } : A - \lambda \ \text{is not Fredholm} \}. \end{equation*}
The Fredholm index of $A$ is defined as the Euler characteristic of $K ( A , \mathcal{X} )$. For example, if $n = 2$, $\operatorname{index}( A ) = \operatorname { dim } \operatorname { Ker } D _ { A } ^ { 0 } - \operatorname { dim } ( \operatorname { Ker } D _ { A } ^ { 1 } / \operatorname { Ran } D _ { A } ^ { 0 } ) + \operatorname { dim } ( {\cal X} / \operatorname { Ran } D _ { A } ^ { 1 } )$. In a Hilbert space, $\sigma _ { \text{Te} } ( A , \mathcal{H} ) = \sigma _ { \text{T} } ( L _ { a } , \mathcal{Q} ( \mathcal{H} ) )$, where $a : = \pi ( A )$ is the coset of $A$ in the Calkin algebra for $\mathcal{H}$.
Example.
If $\mathcal H = H ^ { 2 } ( S ^ { 3 } )$ and $A _ { i } : = M _ { z _ { i } }$ ($i = 1,2$), then $\sigma _ { \text{l}} ( A ) = \sigma _ { \text{le} } ( A ) = \sigma _ { \text{re} } ( A ) = \sigma _ { \text{Te} } ( A ) = S ^ { 3 }$, $\sigma _ { r } ( A ) = \sigma _ { T } ( A ) = \mathbf{B} _ { 4 }$, and $\operatorname{index}( A - \lambda ) = 1$ ($\lambda \in \mathbf{B} _ { 4 }$).
The Taylor spectral and Fredholm theories of multiplication operators acting on Bergman spaces over Reinhardt domains or bounded pseudo-convex domains, or acting on the Hardy spaces over the Shilov boundary of bounded symmetric domains on several complex variables, have been described in [a4], [a3], [a6], [a7], [a8], [a16], [a15], [a19], and [a21]; for Toeplitz operators with $H ^ { \infty }$ symbols acting on bounded pseudo-convex domains, concrete descriptions appear in [a11].
Spectral inclusion.
If $S$ is a subnormal $n$-tuple acting on $\mathcal{H}$ with minimal normal extension $N$ acting on $\mathcal{K}$ (cf. also Normal operator), $\sigma _ { \text{T} } ( N , \mathcal{K} ) \subseteq \sigma _ { \text{T} } ( S , \mathcal{H} ) \subseteq \hat { \sigma } ( N , \mathcal{K} )$ [a14].
Left and right multiplications.
For $A$ and $B$ two commuting $n$-tuples of operators on a Hilbert space $\mathcal{H}$, and 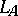 and $R _ { B }$ the associated $n$-tuples of left and right multiplication operators [a5],
and $R _ { B }$ the associated $n$-tuples of left and right multiplication operators [a5],
\begin{equation*} \sigma _ { \operatorname{T} } ( ( L _ { A } , R _ { B } ) , \mathcal{L} ( \mathcal{H} ) ) = \sigma _ { \operatorname{T} } ( A , \mathcal{H} ) \times \sigma _ { T } ( B , \mathcal{H} ) \end{equation*}
and
\begin{equation*} \sigma _ { \text{Te} } ( ( L _ { A } , R _ { B } ) , \mathcal{L} ( \mathcal{H} ) ) = \end{equation*}
\begin{equation*} = [ \sigma _ { \operatorname{Te} } ( A , {\cal H} ) \times \sigma _ { \operatorname{T} } ( B , {\cal H} ) ] \bigcup [ \sigma _ { \operatorname{T} } ( A , {\cal H} ) \times \sigma _ { \operatorname{Te} } ( B , {\cal H} ) ]. \end{equation*}
During the 1980s and 1990s, Taylor spectral theory has received considerable attention; for further details and information, see [a2], [a11], [a20], [a10], [a1]. There is also a parallel "local spectral theory" , described in [a11], [a12] and [a20].
References
| [a1] | E. Albrecht, F.-H. Vasilescu, "Semi-Fredholm complexes" Oper. Th. Adv. Appl. , 11 (1983) pp. 15–39 MR0789629 Zbl 0527.47008 |
| [a2] | C.-G. Ambrozie, F.-H. Vasilescu, "Banach space complexes" , Kluwer Acad. Publ. (1995) MR1357165 Zbl 0837.47009 |
| [a3] | C. Berger, L. Coburn, A. Koranyi, "Opérateurs de Wiener–Hopf sur les spheres de Lie" C.R. Acad. Sci. Paris Sér. A , 290 (1980) pp. 989–991 MR584284 Zbl 0436.47021 |
| [a4] | C. Berger, L. Coburn, "Wiener–Hopf operators on $U _ { 2 }$" Integral Eq. Oper. Th. , 2 (1979) pp. 139–173 MR0543881 Zbl 0434.47019 |
| [a5] | R. Curto, L. Fialkow, "The spectral picture of $( L_{A} , R _ { B } )$" J. Funct. Anal. , 71 (1987) pp. 371–392 MR0880986 Zbl 0626.47018 |
| [a6] | R. Curto, P. Muhly, "$C ^ { * }$-algebras of multiplication operators on Bergman spaces" J. Funct. Anal. , 64 (1985) pp. 315–329 MR0813203 Zbl 0583.46049 |
| [a7] | R. Curto, N. Salinas, "Spectral properties of cyclic subnormal $m$-tuples" Amer. J. Math. , 107 (1985) pp. 113–138 MR778091 |
| [a8] | R. Curto, K. Yan, "The spectral picture of Reinhardt measures" J. Funct. Anal. , 131 (1995) pp. 279–301 MR1345033 Zbl 0826.47002 |
| [a9] | R. Curto, "Spectral permanence for joint spectra" Trans. Amer. Math. Soc. , 270 (1982) pp. 659–665 MR0645336 Zbl 0508.47039 Zbl 0491.47020 |
| [a10] | R. Curto, "Applications of several complex variables to multiparameter spectral theory" J.B. Conway (ed.) B.B. Morrel (ed.) , Surveys of Some Recent Results in Operator Theory II , Pitman Res. Notes in Math. , 192 , Longman Sci. Tech. (1988) pp. 25–90 MR0976843 Zbl 0827.47005 |
| [a11] | J. Eschmeier, M. Putinar, "Spectral decompositions and analytic sheaves" , London Math. Soc. Monographs , Oxford Sci. Publ. (1996) MR1420618 Zbl 0855.47013 |
| [a12] | K. Laursen, M. Neumann, "Introduction to local spectral theory" , London Math. Soc. Monographs , Oxford Univ. Press (2000) MR1747914 Zbl 0957.47004 |
| [a13] | M. Putinar, "Uniqueness of Taylor's functional calculus" Proc. Amer. Math. Soc. , 89 (1983) pp. 647–650 MR718990 |
| [a14] | M. Putinar, "Spectral inclusion for subnormal $n$-tuples" Proc. Amer. Math. Soc. , 90 (1984) pp. 405–406 MR728357 |
| [a15] | N. Salinas, A. Sheu, H. Upmeier, "Toeplitz operators on pseudoconvex domains and foliation $C ^ { * }$-algebras" Ann. of Math. , 130 (1989) pp. 531–565 MR1025166 |
| [a16] | N. Salinas, "The $\overline { \partial }$-formalism and the $C ^ { * }$-algebra of the Bergman $n$-tuple" J. Oper. Th. , 22 (1989) pp. 325–343 MR1043731 |
| [a17] | J.L. Taylor, "A joint spectrum for several commuting operators" J. Funct. Anal. , 6 (1970) pp. 172–191 MR0268706 Zbl 0233.47024 |
| [a18] | J.L. Taylor, "The analytic functional calculus for several commuting operators" Acta Math. , 125 (1970) pp. 1–48 MR0271741 Zbl 0233.47025 |
| [a19] | H. Upmeier, "Toeplitz $C ^ { * }$-algebras on bounded symmetric domains" Ann. of Math. , 119 (1984) pp. 549–576 MR744863 |
| [a20] | F.-H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) MR0690957 Zbl 0495.47013 |
| [a21] | U. Venugopalkrishna, "Fredholm operators associated with strongly pseudoconvex domains in $\mathbf{C} ^ { n }$" J. Funct. Anal. , 9 (1972) pp. 349–373 MR0315502 Zbl 0241.47023 |
Taylor joint spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Taylor_joint_spectrum&oldid=14902