Tangle
relative link
A one-dimensional manifold properly embedded in a  -ball,
-ball, 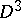 .
.
Two tangles are considered equivalent if they are ambient isotopic with their boundary fixed. An  -tangle has
-tangle has 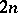 points on the boundary; a link is a
points on the boundary; a link is a  -tangle. The term arcbody is used for a one-dimensional manifold properly embedded in a
-tangle. The term arcbody is used for a one-dimensional manifold properly embedded in a  -dimensional manifold.
-dimensional manifold.
Tangles can be represented by their diagrams, i.e. regular projections into a  -dimensional disc with additional over- and under-information at crossings. Two tangle diagrams represent equivalent tangles if they are related by Reidemeister moves (cf. Reidemeister theorem). The word "tangle" is often used to mean a tangle diagram or part of a link diagram.
-dimensional disc with additional over- and under-information at crossings. Two tangle diagrams represent equivalent tangles if they are related by Reidemeister moves (cf. Reidemeister theorem). The word "tangle" is often used to mean a tangle diagram or part of a link diagram.
The set of  -tangles forms a monoid; the identity tangle and composition of tangles is illustrated in Fig.a1.
-tangles forms a monoid; the identity tangle and composition of tangles is illustrated in Fig.a1.

Figure: t130030a
Several special families of tangles have been considered, including the rational tangles, the algebraic tangles and the periodic tangles (see Rotor). The  -braid group is a subgroup of the monoid of
-braid group is a subgroup of the monoid of  -tangles (cf. also Braided group). One has also considered framed tangles and graph tangles. The category of tangles, with boundary points as objects and tangles as morphisms, is important in developing quantum invariants of links and
-tangles (cf. also Braided group). One has also considered framed tangles and graph tangles. The category of tangles, with boundary points as objects and tangles as morphisms, is important in developing quantum invariants of links and  -manifolds (e.g. Reshetikhin–Turaev invariants). Tangles are also used to construct topological quantum field theories.
-manifolds (e.g. Reshetikhin–Turaev invariants). Tangles are also used to construct topological quantum field theories.
References
| [a1] | F. Bonahon, L. Siebenmann, "Geometric splittings of classical knots and the algebraic knots of Conway" , Lecture Notes , 75 , London Math. Soc. (to appear) |
| [a2] | J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon Press (1969) pp. 329–358 |
| [a3] | M. Lozano, "Arcbodies" Math. Proc. Cambridge Philos. Soc. , 94 (1983) pp. 253–260 |
Tangle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangle&oldid=15693