Tangent
The trigonometric function
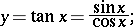 |
another notation is: tg. Its domain of definition is the entire number axis with the exception of the points  ,
,  . The tangent is an unbounded, odd and periodic (with
. The tangent is an unbounded, odd and periodic (with  as the smallest positive period) function. The tangent and the cotangent are connected by the relation
as the smallest positive period) function. The tangent and the cotangent are connected by the relation
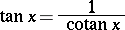 |
The inverse function to the tangent is called the arctangent.
The derivative of the tangent is:
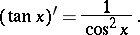 |
The indefinite integral of the tangent is:
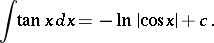 |
The tangent has a series expansion:
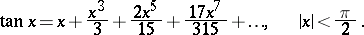 |
The tangent of a complex argument  is a meromorphic function with zeros at the points
is a meromorphic function with zeros at the points  , where
, where  .
.
Comments
The general term in the series expansion of the tangent is:
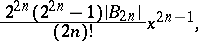 |
where  are the Bernoulli numbers.
are the Bernoulli numbers.
See also Trigonometric functions.
The addition formula of the tangent is:
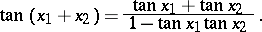 |
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1965) pp. 71ff |
Tangent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent&oldid=15300