T-ideal
of a free associative algebra
A totally invariant ideal, that is, an ideal invariant under all endomorphisms. The set of all polynomial identities of an arbitrary variety of associative algebras over a field 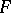 (cf. Associative rings and algebras) forms a
(cf. Associative rings and algebras) forms a 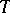 -ideal in the countably-generated free algebra
-ideal in the countably-generated free algebra 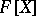 ,
, 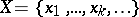 . Thus, there exists a one-to-one correspondence between the
. Thus, there exists a one-to-one correspondence between the 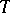 -ideals of
-ideals of 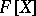 and the varieties of associative algebras over
and the varieties of associative algebras over 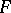 . If
. If 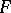 has characteristic
has characteristic  , then for every
, then for every 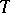 -ideal
-ideal 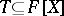 there exists a natural number
there exists a natural number 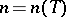 such that certain powers of elements of
such that certain powers of elements of 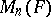 are elements of
are elements of 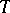 , and only they, where
, and only they, where 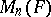 is the ideal of identities of the algebra
is the ideal of identities of the algebra 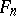 of all
of all 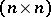 -matrices over
-matrices over 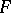 . In this case a
. In this case a 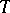 -ideal can also be defined as a (two-sided) ideal that is closed under all differentiations of the free algebra. The quotient algebra
-ideal can also be defined as a (two-sided) ideal that is closed under all differentiations of the free algebra. The quotient algebra 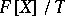 is a PI-algebra with
is a PI-algebra with 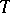 as set of polynomial identities. It is called the relatively free algebra (or generic algebra) with
as set of polynomial identities. It is called the relatively free algebra (or generic algebra) with 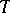 -ideal of identities
-ideal of identities 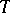 (and is a free algebra in the variety of algebras defined by the identities in
(and is a free algebra in the variety of algebras defined by the identities in 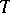 ). The algebra
). The algebra 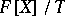 has no zero divisors if and only if
has no zero divisors if and only if 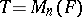 for some natural number
for some natural number  . Every
. Every 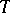 -ideal
-ideal 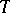 of a free associative algebra is primary.
of a free associative algebra is primary.
The 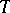 -ideals of a free associative algebra on infinitely many generators over a field of characteristic zero form a free semi-group under the operation of multiplication of ideals. In this case a
-ideals of a free associative algebra on infinitely many generators over a field of characteristic zero form a free semi-group under the operation of multiplication of ideals. In this case a 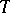 -ideal can be defined as an ideal invariant under all automorphisms of the free algebra.
-ideal can be defined as an ideal invariant under all automorphisms of the free algebra.
For the question as to whether every 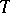 -ideal of
-ideal of 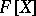 is the totally invariant closure of finitely many elements (Specht's problem) see also Variety of rings.
is the totally invariant closure of finitely many elements (Specht's problem) see also Variety of rings.
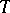 -ideals can be defined for non-associative algebras (Lie, alternative and others) by analogy with the associative case.
-ideals can be defined for non-associative algebras (Lie, alternative and others) by analogy with the associative case.
References
| [1] | C. Procesi, "Rings with polynomial identities" , M. Dekker (1973) |
| [2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [3] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
| [4] | S. Amitsur, "The 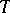 -ideals of the free ring" J. London Math. Soc. , 30 (1955) pp. 470–475 -ideals of the free ring" J. London Math. Soc. , 30 (1955) pp. 470–475 |
| [5] | W. Specht, "Gesetze in Ringen I" Math. Z. , 52 (1950) pp. 557–589 |
| [6] | G. Bergman, J. Lewin, "The semigroup of ideals of a fir is (usually) free" J. London Math. Soc. (2) , 11 : 1 (1975) pp. 21–31 |
Comments
A.R. Kemer has positively solved the Specht problem in the case of characteristic zero (see Variety of rings). He has also introduced the notion of a 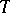 -prime ideal, i.e. if
-prime ideal, i.e. if 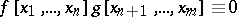 (
(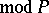 ) for a
) for a 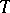 -ideal
-ideal 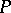 , with different variables in
, with different variables in 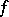 and
and 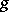 , then either
, then either 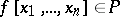 or
or 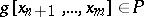 . Similarly, for a
. Similarly, for a 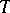 -nilpotent ideal. He has shown that for every
-nilpotent ideal. He has shown that for every 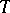 -ideal
-ideal 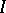 there exists a
there exists a  -ideal
-ideal 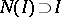 such that
such that 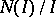 is
is 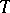 -nilpotent and
-nilpotent and 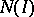 is a finite product of
is a finite product of  -prime ideals.
-prime ideals.
References
| [a1] | A.R. Kemer, "Solution of the finite basis problem" Soviet Math. Dokl. , 37 (1988) pp. 60–64 Dokl. Akad. Nauk SSSR , 298 (1988) pp. 273–277 |
| [a2] | A.R. Kemer, "Finite basis property of identities of associative algebras" Algebra and Logic , 26 (1987) pp. 362–397 Algebra i Logika , 26 (1987) pp. 597–641 |
| [a3] | E. Formanek, "The polynomial identities and invariants of 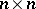 matrices" , Amer. Math. Soc. (1991) matrices" , Amer. Math. Soc. (1991) |
T-ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=T-ideal&oldid=14127