System of common representatives
From Encyclopedia of Mathematics
system of simultaneous representatives
A set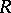 
of cardinality 
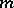which is a system of different representatives for each of the 
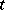families of subsets 
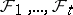of a given set 
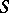, each of which consists of 
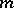elements. Suppose that 
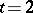, that 
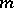is finite, let 
, 
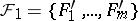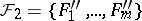, and let 
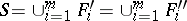. A system of common representatives for 
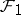and 
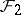exists if and only if no 
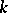sets of the family 
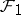are contained in fewer than 
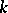sets of 
, for each 
. This theorem is valid also for infinite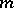 
, provided all the subsets in the families 
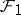and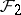 
are finite. Conditions for the existence of a system of common representatives are known for 
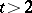, but are more complicated to formulate.
References
| [1] | M. Hall, "Combinatorial theory" , Wiley (1986) |
Comments
References
| [a1] | H.J. Ryser, "Combinatorial mathematics" , Math. Assoc. Amer. (1963) |
| [a2] | L. Mirsky, "Transversal theory" , Acad. Press (1971) |
| [a3] | M. Aigner, "Combinatorial theory" , Springer (1979) pp. Chapt. II (Translated from German) |
How to Cite This Entry:
System of common representatives. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_common_representatives&oldid=16892
System of common representatives. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_common_representatives&oldid=16892
This article was adapted from an original article by V.E. Tarakanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article