Syracuse problem
 -problem, Collatz problem, Hasse algorithm, Hasse–Collatz problem, Kakutani problem, Ulam problem
-problem, Collatz problem, Hasse algorithm, Hasse–Collatz problem, Kakutani problem, Ulam problem
This problem concerns the iteration of the Collatz mapping that sends a positive integer  to
to  (
( even) or to
even) or to  (
( odd). The
odd). The  -conjecture (also called the Collatz conjecture) asserts that for any starting value
-conjecture (also called the Collatz conjecture) asserts that for any starting value 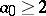 there is some iterate
there is some iterate 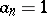 .
.
Some examples are:
a) 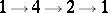 ;
;
b)  ;
;
c) 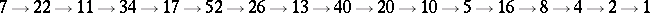 .
.
If 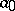 is allowed to be a negative integer, the conjecture is not true, as is shown by the example
is allowed to be a negative integer, the conjecture is not true, as is shown by the example  . In other words: the Collatz conjecture with
. In other words: the Collatz conjecture with 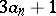 replaced by
replaced by 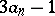 does not hold.
does not hold.
This conjecture is generally attributed to L. Collatz, who studied similar problems in the 1930s. It has been numerically verified for all 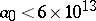 [a5]. The conjecture is unsolved (1996) and apparently extremely difficult despite its simple appearance. General references and surveys on the problem are [a3], [a4], [a6].
[a5]. The conjecture is unsolved (1996) and apparently extremely difficult despite its simple appearance. General references and surveys on the problem are [a3], [a4], [a6].
There is no periodic orbit of the Collatz mapping of period less than  , except the orbit
, except the orbit 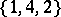 . The set of positive integers
. The set of positive integers 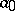 that have some iterate
that have some iterate  less than
less than 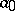 has density one. At least
has density one. At least 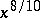 of all positive integers
of all positive integers 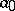 less than
less than  have some iterate
have some iterate 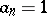 , [a1].
, [a1].
J.H. Conway [a2] showed that a certain generalization of the 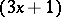 -problem is non-computable. He defined a particular mapping
-problem is non-computable. He defined a particular mapping 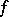 from the positive integers into the positive integers of the form
from the positive integers into the positive integers of the form 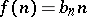 , in which
, in which  is periodic (modulo some
is periodic (modulo some 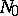 ) for a fixed modulus
) for a fixed modulus 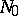 , which has the property that the set
, which has the property that the set
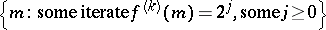 |
is recursively enumerable but not recursive.
References
| [a1] | D. Applegate, J.C. Lagarias, "Density bounds for the 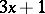 problem II. Krasikov inequalities" Math. Comp. , 64 (1995) pp. 427–438 problem II. Krasikov inequalities" Math. Comp. , 64 (1995) pp. 427–438 |
| [a2] | J.H. Conway, "Unpredictable Iterations" , Proc. 1972 Number Theory Conf. Univ. Colorado, Boulder (1972) pp. 49–52 |
| [a3] | R.K. Guy, "Unsolved problems in number theory" , Springer (1994) pp. Problem E16 (Edition: Second) |
| [a4] | J.C. Lagarias, "The 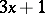 problem and its generalizations" Amer. Math. Monthly , 92 (1985) pp. 3–23 problem and its generalizations" Amer. Math. Monthly , 92 (1985) pp. 3–23 |
| [a5] | G. Leavens, M. Vermeulen, "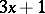 search programs" Computers & Mathematics, with Applications , 24 : 11 (1992) pp. 79–99 search programs" Computers & Mathematics, with Applications , 24 : 11 (1992) pp. 79–99 |
| [a6] | H.A. Müller, "Das "3n+1" Problem" Mitteil. Math. Ges. Hamburg , 12 (1991) pp. 231–251 |
Syracuse problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Syracuse_problem&oldid=11881