Symplectic space
An odd-dimensional projective space 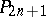 over a field
over a field  endowed with an involutory relation which is a null polarity; it is denoted by
endowed with an involutory relation which is a null polarity; it is denoted by 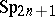 .
.
Let 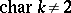 . The absolute null polarity in
. The absolute null polarity in  can always be written in the form
can always be written in the form  , where
, where 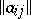 is a skew-symmetric matrix
is a skew-symmetric matrix 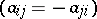 . In vector form, the absolute null polarity can be written in the form
. In vector form, the absolute null polarity can be written in the form 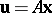 , where
, where 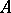 is a skew-symmetric operator whose matrix, in a suitable basis, reduces to the form
is a skew-symmetric operator whose matrix, in a suitable basis, reduces to the form
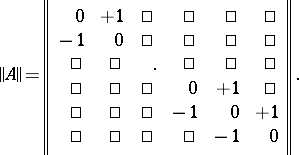 |
In this case the absolute null polarity takes the canonical form
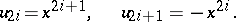 |
The absolute null polarity induces a bilinear form, written in canonical form as follows:
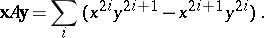 |
Collineations of  that commute with its null polarity are called symplectic transformations; the operators defining these collineations are called symplectic. The above canonical form of
that commute with its null polarity are called symplectic transformations; the operators defining these collineations are called symplectic. The above canonical form of 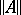 defines the square matrix of order
defines the square matrix of order  of a symplectic operator
of a symplectic operator 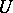 whose elements satisfy the conditions
whose elements satisfy the conditions
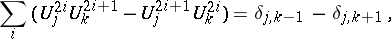 |
where 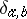 is the Kronecker delta. Such a matrix is called symplectic; its determinant is equal to one. The symplectic transformations form a group, which is a Lie group.
is the Kronecker delta. Such a matrix is called symplectic; its determinant is equal to one. The symplectic transformations form a group, which is a Lie group.
Every point of the space  lies in its polar hyperplane with respect to the absolute null polarity. One can also define polar subspaces in
lies in its polar hyperplane with respect to the absolute null polarity. One can also define polar subspaces in  . The manifold of self-polar
. The manifold of self-polar  -spaces of
-spaces of 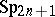 is called its absolute linear complex. In this context, a symplectic group is also called a (linear) complex group.
is called its absolute linear complex. In this context, a symplectic group is also called a (linear) complex group.
Every pair of straight lines, and their polar 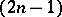 -spaces in the null polarity, define a unique symplectic invariant in
-spaces in the null polarity, define a unique symplectic invariant in 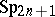 with respect to the group of symplectic transformations of this space. Through every point of each line there passes a transversal of this line and
with respect to the group of symplectic transformations of this space. Through every point of each line there passes a transversal of this line and  -spaces, which defines a projective quadruple of points. This is the geometrical interpretation of a symplectic invariant, which asserts the equality of the cross ratios of these quadruples of points.
-spaces, which defines a projective quadruple of points. This is the geometrical interpretation of a symplectic invariant, which asserts the equality of the cross ratios of these quadruples of points.
The symplectic  -dimensional space admits an interpretation in hyperbolic space and this indicates, among other things, a connection between symplectic and hyperbolic spaces. Thus, the group of symplectic transformations of
-dimensional space admits an interpretation in hyperbolic space and this indicates, among other things, a connection between symplectic and hyperbolic spaces. Thus, the group of symplectic transformations of 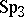 is isomorphic to the group of motions of the hyperbolic space
is isomorphic to the group of motions of the hyperbolic space 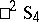 . In this interpretation, the symplectic invariant is related to the distance between points in hyperbolic space.
. In this interpretation, the symplectic invariant is related to the distance between points in hyperbolic space.
References
| [1] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
The notation 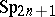 for the symplectic geometry in
for the symplectic geometry in 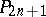 is not usual. By
is not usual. By 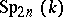 one denotes the symplectic group in the linear space
one denotes the symplectic group in the linear space 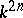 provided with an alternating (i.e. skew-symmetric) bilinear form. The corresponding group of projectivities in
provided with an alternating (i.e. skew-symmetric) bilinear form. The corresponding group of projectivities in 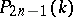 is denoted by
is denoted by 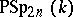 ; this is the group referred to in the main article above, and it is called the projective symplectic group.
; this is the group referred to in the main article above, and it is called the projective symplectic group.
The polar subspaces, or isotropic subspaces, as they are also called, in a projective space with a null polarity form an example of what is called a polar geometry (cf. also Polar space; see ). In J. Tits' theory of buildings, the symplectic spaces interpreted as polar geometries are buildings of type 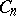 (see [a2] and Tits building).
(see [a2] and Tits building).
References
| [a1a] | F.D. Veldkamp, "Polar geometry" Indag. Math. , 21 (1959) pp. 512–551 |
| [a1b] | F.D. Veldkamp, "Polar geometry" Indag. Math. , 22 (1960) pp. 207–212 |
| [a2] | J. Tits, "Buildings of spherical type and finite BN-pairs" , Lect. notes in math. , 386 , Springer (1974) |
| [a3] | R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) |
| [a4] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1963) |
| [a5] | E. Artin, "Geometric algebra" , Interscience (1957) pp. Chapt. II |
| [a6] | O.T. O'Meara, "Symplectic groups" , Amer. Math. Soc. (1978) |
| [a7] | H. Weyl, "The classical groups" , Princeton Univ. Press (1946) pp. 120 |
| [a8] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 69–70 |
| [a9] | V. Guillemin, S. Sternberg, "Symplectic techniques in physics" , Cambridge Univ. Press (1984) |
| [a10] | A.J. Hahn, O.T. O'Meara, "The classical groups and 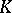 -theory" , Springer (1989) -theory" , Springer (1989) |
| [a11] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French) |
Symplectic space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symplectic_space&oldid=14721