Symplectic homogeneous space
A symplectic manifold 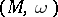 together with a transitive Lie group
together with a transitive Lie group 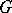 of automorphisms of
of automorphisms of 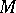 . The elements of the Lie algebra
. The elements of the Lie algebra 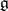 of
of 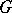 can be regarded as symplectic vector fields on
can be regarded as symplectic vector fields on 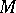 , i.e. fields
, i.e. fields 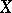 that preserve the symplectic
that preserve the symplectic  -form
-form  :
:
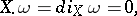 |
where the dot denotes the Lie derivative, 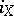 is the operation of interior multiplication by
is the operation of interior multiplication by 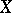 and
and 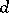 is the exterior differential. A symplectic homogeneous space is said to be strictly symplectic if all fields
is the exterior differential. A symplectic homogeneous space is said to be strictly symplectic if all fields 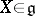 are Hamiltonian, i.e.
are Hamiltonian, i.e. 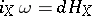 , where
, where 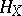 is a function on
is a function on 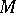 (the Hamiltonian of
(the Hamiltonian of 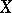 ) that can be chosen in such a way that the mapping
) that can be chosen in such a way that the mapping 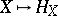 is a homomorphism from the Lie algebra
is a homomorphism from the Lie algebra 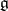 to the Lie algebra of functions on
to the Lie algebra of functions on  with respect to the Poisson bracket. An example of a strictly-symplectic homogeneous space is the orbit
with respect to the Poisson bracket. An example of a strictly-symplectic homogeneous space is the orbit 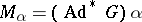 of the Lie group
of the Lie group 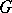 relative to its co-adjoint representation
relative to its co-adjoint representation 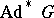 in the space
in the space 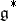 of linear forms on
of linear forms on 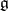 , passing through an arbitrary point
, passing through an arbitrary point 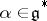 . The invariant symplectic
. The invariant symplectic  -form
-form 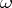 on
on 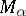 is given by the formula
is given by the formula
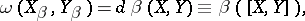 |
where 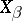 ,
, 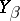 are the values of the vector fields
are the values of the vector fields 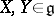 at
at 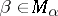 . The field
. The field  has Hamiltonian
has Hamiltonian 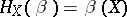 .
.
For an arbitrary strictly-symplectic homogeneous space 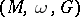 there is the
there is the 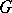 -equivariant moment mapping
-equivariant moment mapping
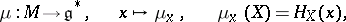 |
which maps  onto the orbit
onto the orbit 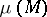 of
of 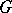 in
in 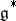 and is a local isomorphism of symplectic manifolds. Thus, every strictly-symplectic homogeneous space of
and is a local isomorphism of symplectic manifolds. Thus, every strictly-symplectic homogeneous space of 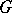 is a covering over an orbit of
is a covering over an orbit of 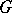 in the co-adjoint representation.
in the co-adjoint representation.
The simply-connected symplectic homogeneous spaces with a simply-connected, but not necessarily effectively-acting automorphism group 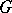 are in one-to-one correspondence with the orbits of the natural action of
are in one-to-one correspondence with the orbits of the natural action of 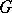 on the space
on the space 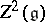 of closed
of closed  -forms on its Lie algebra
-forms on its Lie algebra 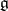 . The correspondence is defined in the following way. The kernel
. The correspondence is defined in the following way. The kernel 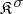 of any
of any  -form
-form 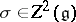 is a subalgebra of
is a subalgebra of 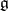 . The connected subgroup
. The connected subgroup 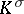 of the Lie group
of the Lie group 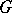 corresponding to
corresponding to  is closed and defines a simply-connected homogeneous space
is closed and defines a simply-connected homogeneous space 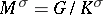 . The form
. The form 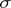 determines a non-degenerate
determines a non-degenerate  -form on the tangent space
-form on the tangent space 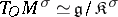 at a point
at a point 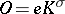 of the manifold
of the manifold 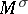 , which extends to a
, which extends to a 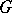 -invariant symplectic form
-invariant symplectic form 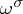 on
on 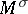 . Thus, to the form
. Thus, to the form 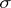 one assigns the simply-connected symplectic homogeneous space
one assigns the simply-connected symplectic homogeneous space 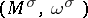 . If
. If 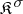 contains no ideals of
contains no ideals of 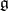 , then the action of
, then the action of 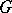 on
on 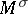 is locally effective. Two symplectic homogeneous spaces
is locally effective. Two symplectic homogeneous spaces 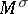 and
and 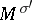 are isomorphic if and only if the forms
are isomorphic if and only if the forms 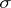 ,
, 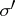 belong to the same orbit of
belong to the same orbit of 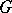 on
on 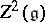 . For an exact
. For an exact  -form
-form 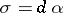 , the symplectic homogeneous space
, the symplectic homogeneous space 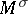 is identified with the universal covering of the symplectic homogeneous space
is identified with the universal covering of the symplectic homogeneous space 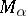 , which is the orbit of a point
, which is the orbit of a point 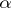 in the co-adjoint representation. If
in the co-adjoint representation. If 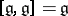 , then the orbit
, then the orbit 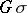 of any point
of any point 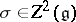 is canonically provided with the structure of a symplectic homogeneous space, and any symplectic homogeneous space of a simply-connected group
is canonically provided with the structure of a symplectic homogeneous space, and any symplectic homogeneous space of a simply-connected group 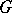 is isomorphic to the covering over one of these orbits. In particular,
is isomorphic to the covering over one of these orbits. In particular, 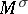 is the universal covering of
is the universal covering of 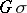 .
.
Let 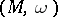 be a compact symplectic homogeneous space of a simply-connected connected group
be a compact symplectic homogeneous space of a simply-connected connected group 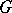 whose action is locally effective. Then
whose action is locally effective. Then 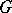 is the direct product of a semi-simple compact group
is the direct product of a semi-simple compact group 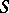 and a solvable group
and a solvable group 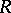 isomorphic to the semi-direct product of an Abelian subgroup and an Abelian normal subgroup, and the symplectic homogeneous space
isomorphic to the semi-direct product of an Abelian subgroup and an Abelian normal subgroup, and the symplectic homogeneous space 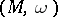 decomposes into the direct product of symplectic homogeneous spaces with automorphism groups
decomposes into the direct product of symplectic homogeneous spaces with automorphism groups 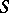 and
and 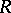 , respectively.
, respectively.
A symplectic group space is a special type of symplectic homogeneous space. It consists of a Lie group together with a left-invariant symplectic form 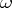 . It is known that for a Lie group admitting a left-invariant symplectic form, reductivity implies commutativity, and unimodularity implies solvability. All such groups of dimension
. It is known that for a Lie group admitting a left-invariant symplectic form, reductivity implies commutativity, and unimodularity implies solvability. All such groups of dimension 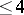 are solvable, but from dimension 6 onwards there are unsolvable symplectic group spaces [3].
are solvable, but from dimension 6 onwards there are unsolvable symplectic group spaces [3].
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | V. Guillemin, S. Sternberg, "Geometric asymptotics" , Amer. Math. Soc. (1977) |
| [3] | B.-Y. Chu, "Symplectic homogeneous spaces" Trans. Amer. Math. Soc. , 197 (1974) pp. 145–159 |
| [4] | Ph.B. Zwart, W.M. Boothby, "On compact, homogeneous symplectic manifolds" Ann. Inst. Fourier , 30 : 1 (1980) pp. 129–157 |
| [5] | N.E. Hurt, "Geometric quantization in action" , Reidel (1983) |
| [6] | D.V. Alekseevskii, A.M. Vinogradov, V.V. Lychagin, "The principal ideas and methods of differential geometry" , Encycl. Math. Sci. , 28 , Springer (Forthcoming) pp. Chapt. 4, Sect. 5 (Translated from Russian) |
Comments
See Lie differentiation for the definitions of Lie derivative and interior multiplication.
Symplectic homogeneous space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symplectic_homogeneous_space&oldid=14939