Symplectic group
One of the classical groups, defined as the group of automorphisms of a skew-symmetric bilinear form 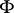 on a left
on a left 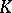 -module
-module 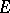 , where
, where 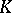 is a commutative ring (cf. Classical group). In the case when
is a commutative ring (cf. Classical group). In the case when 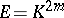 and the matrix of
and the matrix of 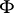 with respect to the canonical basis
with respect to the canonical basis 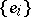 of
of 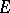 has the form
has the form
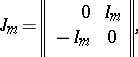 |
where 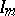 is the identity matrix of order
is the identity matrix of order 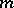 , the corresponding symplectic group is called the symplectic group of
, the corresponding symplectic group is called the symplectic group of 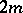 variables over the ring
variables over the ring 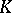 and is denoted by
and is denoted by 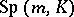 or
or 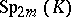 . The matrix of any automorphism in
. The matrix of any automorphism in 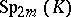 with respect to
with respect to 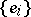 is called a symplectic matrix.
is called a symplectic matrix.
Let 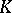 be a field and
be a field and 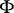 a non-degenerate skew-symmetric bilinear form on an
a non-degenerate skew-symmetric bilinear form on an  -dimensional vector space
-dimensional vector space 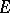 over
over 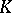 . If
. If  is even, then the symplectic group associated with
is even, then the symplectic group associated with 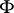 is isomorphic to
is isomorphic to 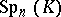 and is generated by all linear transformations of
and is generated by all linear transformations of 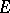 of the form
of the form 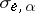 , given by
, given by
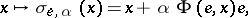 |
where 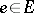 ,
, 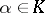 . Linear transformations of the form
. Linear transformations of the form 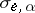 are called symplectic transvections, or translations in the direction of the line
are called symplectic transvections, or translations in the direction of the line 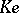 . The centre
. The centre 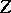 of
of  consists of the matrices
consists of the matrices 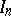 and
and 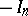 if
if 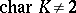 , and
, and 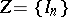 if
if  . The quotient group
. The quotient group 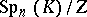 is called the projective symplectic group and is denoted by
is called the projective symplectic group and is denoted by 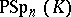 . All projective symplectic groups are simple, except
. All projective symplectic groups are simple, except
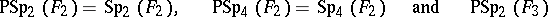 |
(here 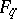 denotes the field of
denotes the field of 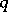 elements) and these are isomorphic to the symmetric groups
elements) and these are isomorphic to the symmetric groups 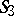 ,
, 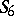 (cf. Symmetric group) and the alternating group
(cf. Symmetric group) and the alternating group 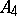 , respectively. The order of
, respectively. The order of 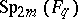 is
is
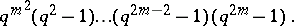 |
The symplectic group 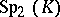 coincides with the special linear group
coincides with the special linear group 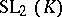 . If
. If 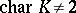 ,
, 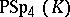 is isomorphic to the quotient group of
is isomorphic to the quotient group of  by its centre, where
by its centre, where 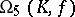 is the commutator subgroup of (index 2 in) the orthogonal group associated with a symmetric bilinear form
is the commutator subgroup of (index 2 in) the orthogonal group associated with a symmetric bilinear form 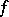 in five variables.
in five variables.
Except when 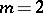 and
and 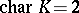 , every automorphism
, every automorphism 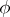 of
of 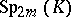 can be written as
can be written as
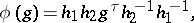 |
where  is an automorphism of the field
is an automorphism of the field 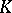 ,
, 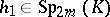 and
and 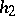 is a linear transformation of the space
is a linear transformation of the space 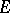 , represented on the basis
, represented on the basis 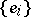 by a matrix of the form
by a matrix of the form
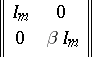 |
(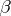 is a non-zero element of
is a non-zero element of 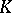 ).
).
 coincides with the group of
coincides with the group of 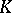 -points of the linear algebraic group
-points of the linear algebraic group 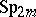 defined by the equation
defined by the equation 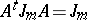 . This algebraic group, also called a symplectic group, is a simple simply-connected linear algebraic group of type
. This algebraic group, also called a symplectic group, is a simple simply-connected linear algebraic group of type 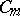 of dimension
of dimension 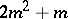 .
.
In the case when 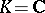 or
or 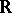 ,
, 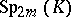 is a connected simple complex (respectively, real) Lie group.
is a connected simple complex (respectively, real) Lie group. 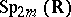 is one of the real forms of the complex symplectic group
is one of the real forms of the complex symplectic group 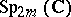 . The other real forms of this group are also sometimes called symplectic groups. These are the subgroups
. The other real forms of this group are also sometimes called symplectic groups. These are the subgroups 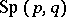 of
of 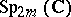 ,
, 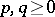 ,
, 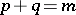 , consisting of those elements of
, consisting of those elements of 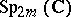 that preserve the Hermitian form
that preserve the Hermitian form
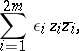 |
where  for
for  and
and 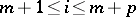 , and
, and  otherwise. The group
otherwise. The group 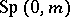 is a compact real form of the complex symplectic group
is a compact real form of the complex symplectic group 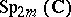 . The symplectic group
. The symplectic group 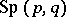 is isomorphic to the group of all linear transformations of the right vector space
is isomorphic to the group of all linear transformations of the right vector space 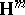 of dimension
of dimension 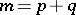 over the division ring
over the division ring  of quaternions that preserve the quaternionic Hermitian form of index
of quaternions that preserve the quaternionic Hermitian form of index 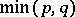 , that is, the form
, that is, the form
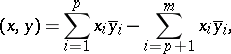 |
where
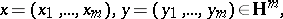 |
and the bar denotes conjugation of quaternions.
References
| [1] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [2] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1973) (Translated from French) |
| [3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [4] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
| [5] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
Comments
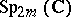 is also simply connected. But
is also simply connected. But 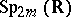 has the homotopy type of
has the homotopy type of 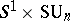 , so that
, so that 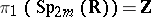 . Here
. Here 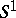 is the circle and
is the circle and 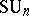 is the special unitary group. The unitary symplectic group
is the special unitary group. The unitary symplectic group 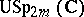 is the intersection (in
is the intersection (in 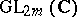 ) of the unitary group
) of the unitary group 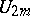 and
and 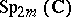 . Topologically,
. Topologically, 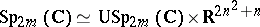 .
.
In Hamiltonian mechanics (cf. Hamilton equations) the phase space is a symplectic manifold, a manifold 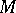 provided with a symplectic form (a closed differential form
provided with a symplectic form (a closed differential form 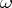 of degree
of degree  which is non-degenerate at each point). If
which is non-degenerate at each point). If 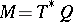 , the cotangent bundle of a configuration space
, the cotangent bundle of a configuration space 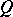 , with local coordinates
, with local coordinates 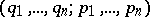 , then the symplectic form
, then the symplectic form 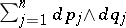 is called canonical. The flow of a Hamiltonian system leaves the symplectic form invariant. As a consequence, its tangent mapping at a fixed point belongs to the symplectic group of the tangent space.
is called canonical. The flow of a Hamiltonian system leaves the symplectic form invariant. As a consequence, its tangent mapping at a fixed point belongs to the symplectic group of the tangent space.
Symplectic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symplectic_group&oldid=17707