Symmetrization method
(in function theory)
One of the methods for solving extremal problems in the geometric theory of functions. Underlying the method is the notion of symmetrization of closed and open sets of the  -dimensional Euclidean space. Symmetrization methods in function theory were first applied in the study of the properties of the transfinite diameter (see [1]), somewhat later to the solution of the Carleman–Milloux problem (see [2]) and were then used quite widely (see [3]–[6], [9]).
-dimensional Euclidean space. Symmetrization methods in function theory were first applied in the study of the properties of the transfinite diameter (see [1]), somewhat later to the solution of the Carleman–Milloux problem (see [2]) and were then used quite widely (see [3]–[6], [9]).
The use of symmetrization methods in function theory is based on the monotone nature of the change of the capacity and interior radius of a domain under various forms of symmetrization. The possibility of applying symmetrization methods in solving extremal problems in the geometric theory of functions results from a definite symmetry of the extremal transformations. Based on the property of non-decrease of the interior radius of a domain under symmetrization relative to a line or ray and using the theorem on the change of the interior radius of a domain under transformation by a regular function, the following symmetrization principle was obtained (see [4]): If the function 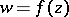 ,
, 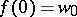 ,
, 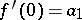 , is regular in the disc
, is regular in the disc 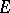 :
: 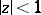 , if
, if 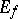 is the set of values of
is the set of values of  in
in 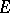 , if
, if 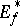 is the result of symmetrization of
is the result of symmetrization of 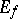 relative to a ray or line passing through
relative to a ray or line passing through 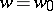 , and if
, and if 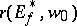 is the interior radius of
is the interior radius of 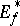 relative to the point
relative to the point  , then
, then
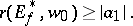 | (*) |
Equality holds in (*) if and only if 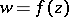 is univalent in
is univalent in 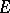 and
and 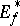 coincides with
coincides with 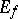 (under Steiner symmetrization) or can be obtained from
(under Steiner symmetrization) or can be obtained from 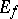 as a result of rotation around
as a result of rotation around 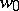 (under Pólya symmetrization). A similar result holds for other forms of symmetrization for which the property of non-decrease of the interior radius holds. Additional research is usually necessary to clarify the condition for equality in (*).
(under Pólya symmetrization). A similar result holds for other forms of symmetrization for which the property of non-decrease of the interior radius holds. Additional research is usually necessary to clarify the condition for equality in (*).
There are generalizations of the symmetrization principle to the case of an annulus and domains of arbitrary connectivity (see [6]). It is fruitful to combine symmetrization methods and other methods for solving extremal problems in the geometric theory of functions (cf. Extremal metric, method of the; Quadratic differential, etc.). A number of covering and distortion theorems for various classes of functions regular in a given domain (univalent, univalent in the mean, weakly 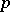 -valent in the disc or in an annulus, etc., see [4]–[6]) have been obtained by this route.
-valent in the disc or in an annulus, etc., see [4]–[6]) have been obtained by this route.
Symmetrization methods have also been applied to the study of properties of spaces of quasi-conformal mappings. This situation is particularly important in view of the limited methods available for studying such mappings. Symmetrization methods allow one to find, among the doubly-connected spatial domains with fixed geometric properties, domains with largest conformal modulus. The determination of such a domain, in its turn, allows one to establish an extremal property of a quasi-conformal mapping. In particular, by the use of a symmetrization method, certain distortion theorems have been established for quasi-conformal mappings in three-dimensional Euclidean space (see [7], [8]).
References
| [1] | G. Faber, "Ueber Potentialtheorie und konforme Abbildung" Sitzungsber. Bayer. Akad. Wiss. Math.-Naturwiss. Kl. , 20 (1920) pp. 49–64 |
| [2] | A. Beurling, "Etudes sur un problème de majoration" L. Carleson (ed.) et al. (ed.) , Collected Works , Birkhäuser (1989) pp. 1–108 (Thèse) |
| [3] | G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) |
| [4] | W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1958) |
| [5] | J.A. Jenkins, "Univalent functions and conformal mappings" , Springer (1958) |
| [6] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [7] | B.V. Shabat, "On the theory of quasiconformal mappings in space" Soviet Math. Dokl. , 1 : 3 (1960) pp. 730–733 Dokl. Akad. Nauk SSSR , 132 : 5 (1960) pp. 1045–1048 |
| [8] | F.W. Gehring, "Symmetrization of rings in space" Trans. Amer. Math. Soc. , 101 : 3 (1961) pp. 499–519 |
| [9] | A. Baernstein, "Integral means, univalent functions and circular symmetrization" Acta Math. , 133 (1974) pp. 139–169 |
Symmetrization method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetrization_method&oldid=16382