Symmetrization

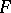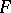The association to each object of an object (of the same class) having some symmetry. Usually symmetrization is applied to closed sets in a Euclidean space 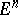(or in a space of constant curvature), and also to mappings; moreover, symmetrization is constructed so that 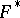continuously depends on 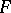. Symmetrization preserves some and monotonely changes other characteristics of an object. Symmetrization is used in geometry, mathematical physics and function theory for the solution of extremal problems. The first symmetrizations were introduced by J. Steiner in 1836 for a proof of an isoperimetric inequality.

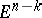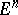Symmetrization relative to a subspace in : For each non-empty section of a set 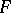by a subspace 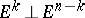one constructs a sphere in 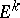with centre 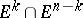and the same 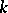-dimensional volume as 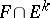; the set 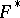formed by these spheres is the result of the symmetrization. Symmetrization relative to a subspace preserves volume and convexity, and does not increase the area of the boundary or the integral of the transversal measure (see [2]). For 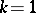this is Steiner symmetrization, for 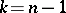it is Schwarz symmetrization.

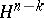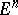Symmetrization relative to a half-space in : For each non-empty section of 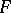by a sphere 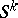with centre on the boundary 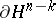and lying in 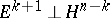, one constructs a spherical cap 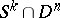(where 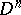is a sphere with centre 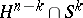) of the same 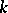-dimensional volume as 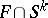; the set 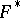formed by these caps is the result of the symmetrization. For 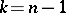this is spherical symmetrization, if 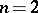it is circular symmetrization.

Symmetrization by displacement: For a convex set 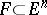one constructs its symmetrization 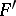relative to a subspace 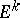; the result of the symmetrization is the set 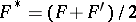, where addition of sets is taken as the vector sum.

Symmetrization by rolling: For a convex body 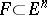its support function is averaged over parallel sections of the unit sphere; the result of symmetrization is the body 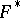recovered from the support function thus obtained.

In 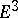Steiner symmetrization preserves volume and does not increase surface area, diameter and capacity; Schwarz symmetrization preserves continuity of the Gaussian curvature of the boundary and does not reduce its minimum; symmetrization relative to a half-space does not increase the fundamental frequency of the domain or the area of the boundary; spherical symmetrization does not increase capacity; symmetrization by displacement preserves the integral of the mean curvature of the boundary and does not reduce the area of the latter; symmetrization by rolling preserves width (see [1], [3]).

In 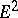Steiner symmetrization does not increase the polar moment of inertia, the exterior radius, the capacity or the fundamental frequency; it does not reduce torsional rigidity or the maximal interior conformal radius (see [3]).

In connection with the manifold applications of symmetrization, the question of convergence of symmetrizations has been considered. The definition of the analogues of symmetrization for non-closed sets permits ramification. On the use of symmetrization in function theory see Symmetrization method.

References

[1]	W. Blaschke, "Kreis und Kugel" , Chelsea, reprint (1949)
[2]	H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)
[3]	G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951)
[4]	K. Leichtweiss, "Konvexe Mengen" , Springer (1979)

Comments

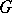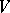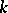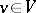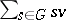Quite generally, if is a finite group acting on a vector space over a field , and , then the symmetrized version of is the element (or 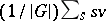). The element

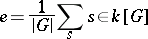is called a symmetrizer. For instance, if 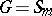is the symmetric group on 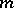letters and 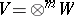, the 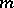-th tensor power of a vector space 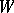(respectively, the vector space of polynomials in 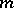variables over 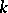), then 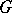acts naturally (by permuting tensor factors, respectively, by permuting the variables) and application of the idempotent to a tensor (respectively, a polynomial) gives the corresponding symmetrized tensor (respectively, symmetrized polynomial). Cf. also Symmetrization (of tensors).

For suitable infinite groups symmetrizers are defined using integrals instead of sums.

If 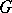is a subgroup of an 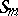, one also considers alternation, i.e. application of the element

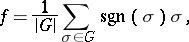where 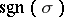is the sign of the permutation 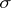. A Young symmetrizer is obtained by symmetrizing with respect to a Young subgroup followed by alternation (with respect to a different Young subgroup, corresponding to a dual partition).

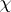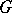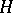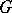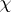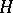More generally, if is any character of a group acting on , and is a subgroup of , then the symmetrizer defined by and is

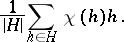The alternator corresponds to the alternating character 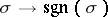of .

References

[a1]	C. Bandle, "Isoperimetric inequalities" P.M. Gruber (ed.) J.M. Wills (ed.) , Convexity and its applications , Birkhäuser (1983) pp. 30–48
[a2]	H.G. Eggleston, "Convexity" , Cambridge Univ. Press (1963)
[a3]	R.V. Benson, "Euclidean geometry and convexity" , McGraw-Hill (1966) pp. Chapt. 6
[a4]	H. Weyl, "The classical groups" , Princeton Univ. Press (1946) pp. 120
[a5]	M. Marcus, "Finite dimensional multilinear algebra" , 1 , M. Dekker (1973) pp. 78ff