Symmetric derivative
From Encyclopedia of Mathematics
A generalization of the concept of derivative to the case of set functions 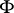 on an
on an  -dimensional Euclidean space. The symmetric derivative at a point
-dimensional Euclidean space. The symmetric derivative at a point  is the limit
is the limit
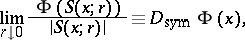 |
where 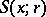 is the closed ball with centre
is the closed ball with centre  and radius
and radius  , if this limit exists. The symmetric derivative of order
, if this limit exists. The symmetric derivative of order  at a point
at a point  of a function
of a function 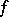 of a real variable is defined as the limit
of a real variable is defined as the limit
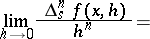 |
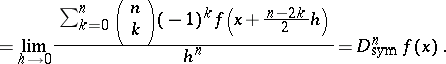 |
A function 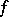 of a real variable has a symmetric derivative of order
of a real variable has a symmetric derivative of order 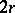 at a point
at a point  ,
,
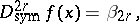 |
if
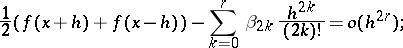 |
and one of order 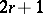 ,
,
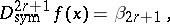 |
if
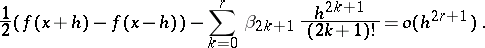 |
If 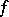 has an
has an  -th order derivative
-th order derivative 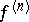 at a point
at a point  , then there is (in both cases) a symmetric derivative at
, then there is (in both cases) a symmetric derivative at  , and it is equal to
, and it is equal to 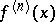 .
.
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1937) (Translated from French) |
| [2] | R.D. James, "Generalized  th primitives" Trans. Amer. Math. Soc. , 76 : 1 (1954) pp. 149–176 th primitives" Trans. Amer. Math. Soc. , 76 : 1 (1954) pp. 149–176 |
Comments
In [1] instead of derivative, "derivate" is used: symmetric derivate.
How to Cite This Entry:
Symmetric derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_derivative&oldid=15476
Symmetric derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_derivative&oldid=15476
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article