Sylow theorems

Three theorems on maximal -subgroups in a finite group, proved by L. Sylow [1] and playing a major role in the theory of finite groups. Sometimes the union of all three theorems is called Sylow's theorem.

Let be a finite group of order , where is a prime number not dividing . Then the following theorems hold.

Sylow's first theorem: contains subgroups of order for all ; moreover, each subgroup of order is a normal subgroup in at least one subgroup of order 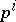. This theorem implies, in particular, the following important results: there is in 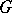a Sylow subgroup of order ; any 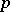-subgroup of 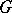is contained in some Sylow 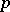-subgroup of order ; the index of a Sylow -subgroup is not divisible by 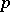; if 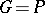is a group of order 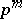, then any of its proper subgroups is contained in some maximal subgroup of order 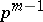and all maximal subgroups of 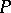are normal.

Sylow's second theorem: All Sylow -subgroups of a finite group are conjugate.

For infinite groups the analogous result is, in general, false.

Sylow's third theorem: The number of Sylow 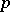-subgroups of a finite group divides the order of the group and is congruent to one modulo .

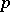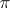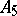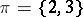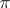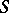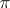For arbitrary sets of prime numbers, analogous theorems have been obtained only for finite solvable groups (see Hall subgroup). For non-solvable groups the situation is different. For example, in the alternating group of degree 5, for there is a Sylow -subgroup of order 6 whose index is divisible by a number from . In addition, in there is a Sylow -subgroup isomorphic to 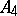and not conjugate with 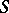. The number of Sylow -subgroups in 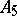does not divide the order of .

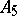References

[1]	L. Sylow, "Théorèmes sur les groupes de substitutions" Math. Ann. , 5 (1872) pp. 584–594
[2]	M. Hall, "Group theory" , Macmillan (1959)