Support of a generalized function
The set of those (and only those) points such that in any neighbourhood of them the generalized function does not vanish. A generalized function  in
in  vanishes in an open set
vanishes in an open set  if
if  for all
for all  . Using a partition of unity it can be proved that if a generalized function
. Using a partition of unity it can be proved that if a generalized function  in
in  vanishes in some neighbourhood
vanishes in some neighbourhood  for each point
for each point  , then
, then 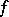 vanishes in
vanishes in 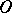 . The union of all neighbourhoods in which
. The union of all neighbourhoods in which  vanishes is called the zero set of
vanishes is called the zero set of 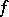 and is denoted by
and is denoted by  . The support of
. The support of  , denoted by
, denoted by  , is the complement of
, is the complement of 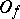 in
in 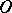 , that is,
, that is, 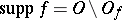 is a closed set in
is a closed set in  . If
. If  is a continuous function in
is a continuous function in  , then an equivalent definition of the support of
, then an equivalent definition of the support of 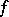 is the following:
is the following:  is the closure in
is the closure in 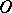 of the complement of the set of points at which
of the complement of the set of points at which  vanishes (cf. Support of a function). For example,
vanishes (cf. Support of a function). For example,  ,
, 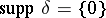 .
.
The singular support ( ) of a generalized function is the set of those (and only those) points such that in any neighbourhood of them the generalized function is not equal to a
) of a generalized function is the set of those (and only those) points such that in any neighbourhood of them the generalized function is not equal to a 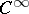 -function. For example,
-function. For example, 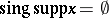 ,
,  .
.
Comments
The notion of a zero set as used above is somewhat unusual and does not agree with the zero set of an ordinary function (not a generalized function) as the set of points where that function assumes the value zero. Of course, the statement "fx=0" has no meaning for generalized functions  .
.
A point  in the support of a generalized function
in the support of a generalized function 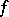 is called an essential point of
is called an essential point of  , cf. [a4].
, cf. [a4].
References
| [a1] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1966) |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) pp. §7.7 |
| [a3] | V.S. Vladimirov, Yu.N. Drozzinov, B.I. Zavialov, "Tauberian theory for generalized functions" , Kluwer (1988) (Translated from Russian) |
| [a4] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 1. Properties and operations , Acad. Press (1964) pp. 5 (Translated from Russian) |
Support of a generalized function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Support_of_a_generalized_function&oldid=12815