Super-manifold
A generalization of the concept of a manifold, on which the functions take values in a commutative superalgebra. The structure of a super-manifold on a differentiable manifold  with structure sheaf
with structure sheaf  is defined by a sheaf
is defined by a sheaf  of commutative superalgebras over the sheaf
of commutative superalgebras over the sheaf  , whereby any point
, whereby any point  possesses a neighbourhood
possesses a neighbourhood  such that the ringed space
such that the ringed space  is isomorphic to
is isomorphic to  , where
, where  is the exterior algebra with
is the exterior algebra with 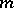 odd generators. Analytic super-manifolds are defined in the same way. The differentiable (or analytic) super-manifolds form a category whose morphisms are the morphisms of ringed spaces that are even on the structure sheaves. The pair (
odd generators. Analytic super-manifolds are defined in the same way. The differentiable (or analytic) super-manifolds form a category whose morphisms are the morphisms of ringed spaces that are even on the structure sheaves. The pair (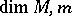 ) is called the dimension of the super-manifold. A super-manifold of the form
) is called the dimension of the super-manifold. A super-manifold of the form  , where
, where 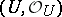 is an open submanifold in
is an open submanifold in  , is called a super-domain of dimension
, is called a super-domain of dimension  . Every super-manifold is locally isomorphic to a super-domain.
. Every super-manifold is locally isomorphic to a super-domain.
If 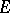 is a vector bundle over
is a vector bundle over 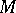 , then the sheaf of sections
, then the sheaf of sections 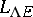 of the bundle
of the bundle 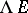 defines the structure of a super-manifold on
defines the structure of a super-manifold on 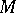 . Every differentiable super-manifold is isomorphic to a super-manifold of the form
. Every differentiable super-manifold is isomorphic to a super-manifold of the form  ; in the complex analytic case this is not true. At the same time there are more morphisms in the category of super-manifolds than in the category of vector bundles.
; in the complex analytic case this is not true. At the same time there are more morphisms in the category of super-manifolds than in the category of vector bundles.
A super-manifold 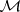 can be defined by a functor
can be defined by a functor 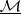 from the category of commutative superalgebras into the category of sets; this functor assigns to the superalgebra
from the category of commutative superalgebras into the category of sets; this functor assigns to the superalgebra 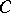 the set
the set 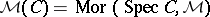 , where
, where 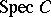 is the set of prime ideals in
is the set of prime ideals in 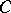 , endowed with the natural sheaf of superalgebras (see Representable functor).
, endowed with the natural sheaf of superalgebras (see Representable functor).
The basic concepts of analysis on differentiable manifolds are also applied to super-manifolds.
The concept of a super-manifold also arose in theoretical physics; it enables one to join particles with Bose–Einstein statistics and Fermi–Dirac statistics into single multiplets, and also enables one to join the internal and dynamic symmetries of gauge theories in a single super-group.
References
| [1] | F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian) |
| [2] | D.A. Leites (ed.) , Seminar on supermanifolds , Kluwer (1990) |
Comments
As noted above, part of the motivation for the study of super-manifolds comes from theoretical physics, in particular supersymmetry and supergravity, [a4]. Not all authors agree that the definitions given above are the best for these purposes, cf. [a2], [a3]. "Desirability axioms" for a "well-behaved" category of super-manifolds are discussed in [a1]. Some definitions of super-manifolds satisfy these axioms, for instance the one above, and some others do not.
References
| [a1] | M. Rothstein, "The axioms of supermanifolds and a new structure arising from them" Trans. Amer. Math. Soc. , 297 (1986) pp. 159–180 |
| [a2] | H.J. Seiert (ed.) C.J.S. Clarke (ed.) A. Rosenblum (ed.) , Mathematical aspects of superspace , Reidel (1984) |
| [a3] | Cl. Bartocci, U. Bruzzo, D. Hernández-Ruipérez, "The geometry of supermanifolds" , Kluwer (1991) |
| [a4] | B. DeWitt, "Supermanifolds" , Cambridge Univ. Press (1984) |
| [a5] | D.A. Leites, "Introduction to the theory of supermanifolds" Russian Math. Surveys , 35 : 1 (1980) pp. 1–64 Uspekhi Mat. Nauk , 35 : 1 (1980) pp. 3–58 |
| [a6] | F.A. Berezin, M.A. Shubin, "The Schrödinger equation" , Kluwer (1991) (Translated from Russian) (Supplement 3: D.A. Leites, Quantization and supermanifolds) |
Super-manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Super-manifold&oldid=16641