Summation of divergent series
The construction of generalized sums of divergent series using summation methods. If, by means of a certain rule  , to the series
, to the series
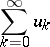 | (*) |
a number has been attached, called the sum of the series, then one says that the series is summable to the sum  by the summation method
by the summation method  , or is
, or is  -summable to the sum
-summable to the sum  , and this fact is denoted by one of the symbols
, and this fact is denoted by one of the symbols
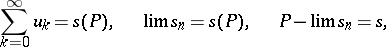 |
where  are the partial sums of the series (*). In this case the number
are the partial sums of the series (*). In this case the number  is also called the
is also called the 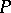 -sum of the series. For example, for the series (*), the sequence
-sum of the series. For example, for the series (*), the sequence 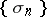 of arithmetical averages of the first
of arithmetical averages of the first  partial sums of the series,
partial sums of the series,
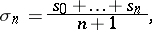 |
can be examined. If 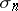 has a limit when
has a limit when  ,
,
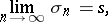 |
then one says that the series (*) is summable to the sum  by the summation method of arithmetical averages (cf. Arithmetical averages, summation method of), which is denoted by the symbol
by the summation method of arithmetical averages (cf. Arithmetical averages, summation method of), which is denoted by the symbol
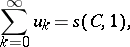 |
or
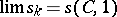 |
(see also Cesàro summation methods).
For this definition of the sum of the series, every convergent series is summable to the sum to which it converges, and, moreover, there exist divergent series that are summable by this method. For example, the series
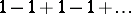 |
is summable by the above method and its  -sum is equal to 1/2.
-sum is equal to 1/2.
The definition of a summation method is usually subject to a series of requirements. For example, it is required that the method should sum a whole class of series; that it should not contradict convergence, i.e. that, being used for a convergent series, it should sum it to the same sum to which the series converges (see Regular summation methods); finally, that the summability of the series
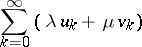 |
to the sum  should follow from the summability of the series
should follow from the summability of the series
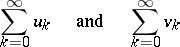 |
by the given method to the sums 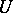 and
and  , respectively (the linearity property). See also Divergent series.
, respectively (the linearity property). See also Divergent series.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 : 1 (1970) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
| [5] | A. Peyerimhoff, "Lectures on summability" , Springer (1969) |
| [6] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [7] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
| [8] | G.M. Petersen, "Regular matrix transformations" , McGraw-Hill (1966) |
Comments
References
| [a1] | C.N. Moore, "Summable series and convergence factors" , Dover, reprint (1966) |
Summation of divergent series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Summation_of_divergent_series&oldid=19002