Submodule
A subset of a module which is a subgroup of its additive group and which is closed under multiplication by elements of the ground ring. In particular, a left (right) ideal of a ring 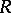 is a submodule of the left (right)
is a submodule of the left (right) 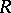 -module
-module 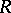 . A submodule distinct from the module itself and the zero submodule is called proper. The set of submodules of a given module, ordered by inclusion, is a complete Dedekind lattice (see Completely-reducible module). If
. A submodule distinct from the module itself and the zero submodule is called proper. The set of submodules of a given module, ordered by inclusion, is a complete Dedekind lattice (see Completely-reducible module). If 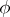 is a homomorphism from a module
is a homomorphism from a module 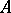 into a module
into a module 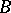 , then the set
, then the set
 |
is a submodule of 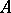 , called the kernel of the homomorphism
, called the kernel of the homomorphism 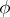 . Each submodule is the kernel of some homomorphism. A submodule is called essential (large or principal) if its intersection with any other non-zero submodule is non-zero. For example, the integers form an essential submodule of the group of rational numbers. Each module is an essential submodule of its injective envelope (see Injective module). A submodule
. Each submodule is the kernel of some homomorphism. A submodule is called essential (large or principal) if its intersection with any other non-zero submodule is non-zero. For example, the integers form an essential submodule of the group of rational numbers. Each module is an essential submodule of its injective envelope (see Injective module). A submodule 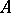 of a module
of a module 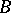 is called inessential (small or co-principal) if for any submodule
is called inessential (small or co-principal) if for any submodule 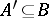 the equation
the equation 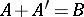 implies
implies  . Any proper submodule of a chain module is inessential. For example, the non-invertible elements in a local ring form an inessential submodule. The sum of all inessential submodules coincides with the intersection of all maximal submodules. A left ideal
. Any proper submodule of a chain module is inessential. For example, the non-invertible elements in a local ring form an inessential submodule. The sum of all inessential submodules coincides with the intersection of all maximal submodules. A left ideal 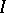 belongs to the Jacobson radical if and only if
belongs to the Jacobson radical if and only if 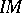 is inessential in
is inessential in 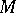 for any finitely-generated left module
for any finitely-generated left module 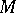 . The elements of a small submodule are non-generating, i.e. any system of generators for a module remains generating after the removal of any of the elements (this of course does not mean that they can all be removed at once). The Jacobson radical of the endomorphism ring of a module coincides with the set of endomorphisms having an inessential image.
. The elements of a small submodule are non-generating, i.e. any system of generators for a module remains generating after the removal of any of the elements (this of course does not mean that they can all be removed at once). The Jacobson radical of the endomorphism ring of a module coincides with the set of endomorphisms having an inessential image.
References
| [1] | F. Kasch, "Modules and rings" , Acad. Press (1982) (Translated from German) |
| [2] | C. Faith, "Algebra" , 1–2 , Springer (1973–1976) |
Submodule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Submodule&oldid=18159